Category:Models
Contents
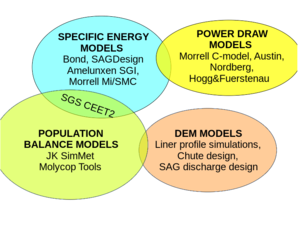
Comminution Models
Computer models are commonly used in comminution can generally be classified into the following four classes:
- Power Models, such as Nordberg and Morrell C-model, are used to predict the power draw of a tumbling mill with a specified charge geometry rotating at a specific speed.
- Specific Energy Models, such as Bond, are used for initial design and for geometallurgy. The mathematics are simple and mostly linear meaning computers can quickly compute hundreds of these types of calculations. These models assume a "standard" particle size distribution (PSD) that can be represented by a single point on the PSD, typically the 80% passing size.
- Population Balance Models, such as JK SimMet and MolyCop Tools, are used mostly for optimization and generally work best when a mill already exists so that the model parameters can be fit to it. The mathematics are more complex than the Power Models and the parameter calibration can be both tedious and time-consuming. These models track the mass flow of each size class independently and do not assume a "standard" particle size distribution, making them suitable for detailed analyses of pebble crushing circuits, for example.
- Discrete Element Modelling (DEM) is generally used for detailed design of specific subsystems in an existing plant. Examples are lifter height and face angle design for mill liners, chute design, and SAG mill discharge system design.
SAGMILLING.COM implements only Power and Specific Energy Models. Other specialized software is needed for population balance or DEM modelling.
Power and Specific Energy Models
Specific Energy and Power models work together by estimating the specific energy required to grind an ore (the specific energy consumption) and the mill power available to grind the ore (the mill power draw). These two types of models in SAGMILLING.COM correspond to:
- Specific energy consumption models are used to estimate the amount of grinding energy required to grind a particular ore, and what throughput can be achieved by passing that ore through a particular set of grinding mills. Examples are the "Optimized Bond/Barratt" models where the circuit specific energy consumption is calculated using the results of Bond work index testing in a laboratory.
- Mill power draw models are used to estimate how much grinding energy can be generated by a particular mill geometry and charge. Examples are the "Austin SAG model" and "Morrell C-model" that predict how much power a mill geometry will draw under a specified set of conditions.
The combination of a circuit specific energy model of an ore's grindability with a "circuit" containing one or more mill power draw models permits the throughput of the particular ore in a particular grinding circuit to be simulated. In the most generalized form, the equations fit together like this:
- Specific energy (kW h/t) = mill power (kW) / throughput (t/h)
Two ways these models can be configured for a given ore (specific energy consumption is a property of that ore) are:
- Knowing the desired throughput allows the circuit mill power to be calculated: kW = (kW h/t) * t/h
- Knowing the circuit power draw allows the throughput to be calculated: t/h = kW / (kW h/t)
History of Specific Energy Consumption Circuit Models
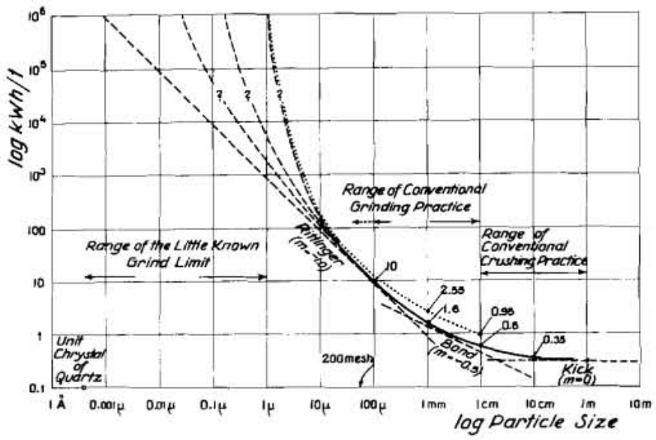
A systematic relationship between energy consumed in grinding and size reduction was proposed by Peter von Rittinger in 1867, yielding the first Power Model and beginning of comminution as a science Lynch & Rowland, 2005. This was followed in 1885 by the theory of Friedrich Kick who proposed a much different power model. Instruments of that age did not allow accurate enough measurements to test the theories Lynch & Rowland, 2005, so the difference between the models was largely of academic interest. Not until instruments for motor power measurement and laboratory grinding mills were standardized in the late 1930's to 1940's were attempts made to bench-mark the theories of von Rittinger and Kick to operating grinding plants (one such attempt was Myers, Michaelson & Bond, AIME 1947). The failure of these rod mill and ball mill bench-mark studies to validate either model led to the development of a "Third Theory" by Fred Bond Bond 1952.
R. Hukki in 1962 showed that all three theories may be special cases of a spectrum of a larger, more generalized, theory where Kick best characterized the coarsest particles (blasting), Bond the middle size ranges (rod and ball milling), and von Rittinger the finest size classes (fine and ultra-fine grinding). Hukki's diagram showing the size spectrum is reproduced below:
Fine grinding models, such as the Isamill signature plots, tend to have widely varying exponents, in the range of -1 to -3 depending on the ore. Metso jar mill tests can be interpreted in a way that also gives a signature plot.
Hukki (among others) related many of the empirical models back to a more fundamental differential equation form, attributed to Walker et al (1937) or Charles (1957):
- dE/dx = -C x-a
where E is energy consumed; x is particle size; and C and a are empirical ore characteristics.
A later model by Stephen Morrell attempted to smoothly merge all three of the earlier models into a single continuum that was fitted to surveys conducted (mostly) in Australasia and Africa. However, the exponents derived by Morrell are very different from the exponents predicted by Hukki and, in the finest size classes where the exponent tends to ~-0.30, do not match observed signature plots from tests involving stirred mills (e.g. Isamills and Vertimills where the exponent ranges between -1 and -3).
A recent testing program Jankovic, Dunar & Mehta, 2010 finds von Rittinger's exponent of -1 provides the best fit to a data set of batch grinding magnetite ore ground down to between 80 µm and 20 µm. There is an issue with the experimental data that the authors do not address: the particle size distributions of the feed and product are not completely parallel in log-log space and the feed appears to have a small surplus of fines. This effect probably does not influence the conclusions:
- "the exponent of the Bond equation (-0.5) is not accurate for prediction of the whole range of test work results [80 µm to 20 µm]. A significantly better fit was obtained using the Rittinger (exponent -1) formula."
- "the best fit of experimental data was obtained with exponents close or equal to -1. Therefore, Morrell’s method [exponent -0.3] is not applicable for batch grinding"
Theory of Specific Energy Consumption Models
Laboratory measurements of the grinding energy required to break rocks are input into empirical formulae, such as Bond's equations, the SGI equations or the "Mi" equations that use results from SMC tests. Different size classes are tested and, in general, the specific energy consumption models use the laboratory parameters to influence the similar size range in the model.
Taggart noted (and Bond adopted) several properties of common size reduction processes that allows modelling as a process of energy consumption by and ore1,2. The underlying observations (and assumptions) of Specific Energy Models are:
- Any particle size distribution can be modelled by a single value. Generally, it is the 80% passing size that is used as being indicative of the entire size distribution.
- Particle size distributions of "normal" size reduction processes produce "similar" particle size curves, generally with the feed and product having the same proportions of "coarse" and "fines" where only the sizes that define coarse and fine are shifted.
Mill Power Draw Models
Mill power models predict the amount of power (measured at the mill shell) that will be drawn by a mill of a particular geometry under particular operating conditions. A variety of models are available for a particular type of mill, and all should give similar answers for most conditions. If mill models give very different power draw predictions, then carefully check that the operating conditions entered are valid and not far outside the calibration range of the models.
In general, the mill power draw models are independent of the ore being processed (ore density matters, but feed and product sizes should not affect power draw if the mill is run properly). The specific energy model uses the ore grindability test results to estimate energy requirements to achieve a particular size reduction, then it calls on the mill power draw model to determine how much energy is actually available. Dividing the energy available by the specific energy consumption results in the throughput.
Pages in category "Models"
The following 22 pages are in this category, out of 22 total.
M
- Mill power draw models
- Model:Amelunxen SGI
- Model:Bond RMBM Model
- Model:Bond-Rowland SSBM
- Model:Bond/Barratt SAB Model
- Model:Bond/Barratt SABC Models
- Model:Bond/Barratt SS SAG
- Model:El Soldado SS SAG
- Model:Morrell HPGR and ball mill
- Model:Morrell Mi SMC SAG
- Model:Morrell SS SAG
- Model:Morrell SSBM
- Model:Raw Bond/Barratt SAB & SABC Model
- Morrell C-model