Nordberg ball mill model
This ball mill and rod mill power draw model is based on a torque model and empirical measurements made by the Nordberg Equipment Company for use by its sales representatives to size grinding mills. Slight differences in the equations used allow rod mills, dry ball mills and wet overflow and grate ball mills to be sized.
History
This model was published by the Nordberg equipment company with versions of it appearing in their "Red Book" equipment sizing manual in the 1970's. The latest version of this model published was by the Outokumpu company (now Outotec) publication "The Science of Comminution" (undated, but probably about 2002).
Inputs
The model requires three inputs in its original form, and a "density corrected" variation includes a fourth input.
- mill effective inside diameter (to calculate Factor A)
- mill fraction filling of the charge (to calculate Factor B)
- mill fraction of critical speed (to calculate Factor C).
- (for density correction) effective density of the mill charge
Output
The model output is the "US horsepower per foot of mill length" where the power is measured at the mill shell. Multiplying this output by the mill effective grinding length and converting the result to modern units of power results in the mill power draw at the shell in kilowatts.
Calculation description
Each of the three original inputs are fit to equations based on the Nordberg published tables that generate, respectively, values for Factor A, Factor B and Factor C which are multiplied together. There are slightly different versions of the Factor B for different styles of mills. The equation presented below is for wet overflow ball mills.
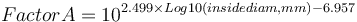
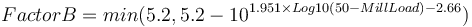
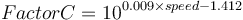
The Outokumpu reference gives the base mill charge density for these formulae as 310 lb/ft3. This translates to a charge density of 5050 kg/m3. Knowing the actual density of the charge allows the correction to be calculated as:
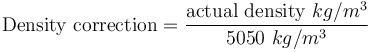
The model result is "horsepower per foot of mill effective grinding length", so multiply the result by the mill EGL to get pinion power draw.
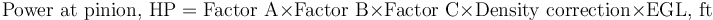
Effective grinding length (EGL)
The effective grinding length of a ball mill is the belly length of the mill inside the mill liners from the inside of the head end liner to the inside of the discharge end liner or grate.
The effective grinding length of a rod mill is the belly length of the mill inside the mill liners from the inside of the head end liner to the inside of the discharge end liner or grate. The length of the rods is expected to be six inches less than the EGL.
Mill manufacturers often describe a different length, the cylinder length or the flange-to-flange length. This flange-to-flange length is usually six inches more than the EGL for overflow mills. The flange-to-flange length may be anywhere between 1.5 and 3 feet longer than the EGL for grate mills (more throughput usually requires deeper discharge chambers behind the grate).