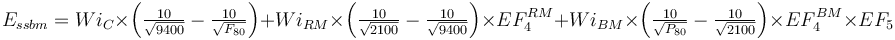Model:Bond-Rowland SSBM
Contents
Bond/Rowland Single Stage Ball Mill Model
This is a multi-stage crushing plant feeding a ball mill model that estimates the specific energy consumption (EBM) using the Rowland interpretation of the classical Bond work index equation including Rowland efficiency factors.
Testwork Required
Formulae
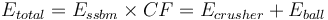
where CF is an optional calibration factor, use 1.0 for normal situations.
The rod mill oversize feed factor (EF4RM) is calculated using the greater of the sample's rod mill or crushing work index (which is usually the WiRM). The optimal feed size and EF4 are both calculated using whichever is greater.
![EF_4^{RM} =\left [ 1 + \left( \frac{ (0.907 \times Wi_{RM} - 7) }{ \left (\frac{F_{80} }{ P_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 16 000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]](/images/math/7/e/9/7e9b49234a38249bd7b36477cdc0e3ef.png)
where:
- F80 = 9400 µm
- P80 = 2100 µm
Both the ball mill and rod mill work index values are used to compute EF4BM: The ball mill work index in the oversize feed factor component and the rod mill work index in the optimal feed size component.
![EF_4^{BM} =\left [ 1 + \left( \frac{(0.907 \times Wi_{BM} - 7) }{ \left (\frac{F_{80} }{ P_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 4000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]](/images/math/a/1/a/a1a63ddfd19337a26911b8e6354d94b3.png)
where:
- F80 = 2100 µm
- P80 = the specified circuit product size, µm
Secondary and tertiary crushers
The model does NOT validate the choice of crushers for the specified sizes; it simply calculates a specific energy based on the power drawn and the throughput dictated by the ball mill circuit. The throughput in the crushing circuit is NOT calculated and the motor sizes are NOT checked to see if they are suitable for the duty presented.
The choice of crushers and arrangement is normally based on volumetric flow and not on power draw. Use a crusher catalogue or another tool, like Metso's Bruno software, to determine the size and arrangement of the crushers ahead of the ball mill(s).
Default parameter values
- Assumed crusher product (T80) size, µm = 9400
- Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P80 and typical ball mill work index test F80).
- To simulate dry ball milling requires the Rowland EF1 factor of 1.3 be entered as the "SSBM calibration factor" in the circuit settings.
Simulating an HPGR circuit
The high pressure grinding roll (HPGR) circuits are becoming common, and they can be considered a variation on the classical single stage ball mill circuit where the final stage of crushing is the HPGR. Simulating HPGR has two differences from a classical SSBM circuit with cone crushers: first is that the crusher product tends to be finer (~4 mm versus 9 mm) and the nature of the product is different.
The particle size curve of HPGR product is "non-standard" according to Bond's root-2 rule, meaning the transfer size for Bond calculations is "synthetic" (same as for SAG mills). To simulate this, refer to the HPGR and ball mill using Bond instructions.