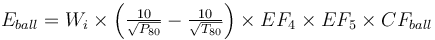Model:Raw Bond/Barratt SAB & SABC Model
Contents
Raw Bond Model
This is a SAG or AG mill plus ball mill model that estimates the specific energy consumption (ESAG) using the 1979 Barratt equation and the classical Bond work index equation including Rowland efficiency factors. The model allows a manual calibration factor on both equations (CFSAG and CFball, respectively).
This formula usually gives higher total circuit specific energy consumption estimates than the other Bond/Barratt models. This is largely due to the absence of a phantom cyclone effect in the equations.
Testwork Required
Formulae
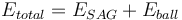
Pebble Crushing
The pebble crusher is considered part of the SAG mill for the purposes of this model. The displayed Epeb value will always be zero, but the displayed Easag will include the shell power of the SAG mill plus the usable power of the pebble crusher.
Unlike other models, there is no explicit benefit to Etotal efficiency due to pebble crushing. This is a conservative assertion and is different from other models where inclusion of pebble crushing causes an immediate improvement in circuit energy efficiency.
Discussion
As with most models, the power split between the SAG and ball mills is evaluated and the transfer size (T80) necessary to balance the power draw between the two stages is estimated. If that transfer size is within the specified limits, then the calculation proceeds to calculate the ESAG and Eball using that transfer size. If the transfer size to balance the power is outside the specified limits, then the transfer size size is forced to the limit and the ESAG and Eball values are then recalculated. SAG-limited circuits (where the T80 hits the upper limit) will result in the ball mill over-grinding unless (in the case of a variable speed mill) the ball mill speed is reduced to control the grind size. Ball-limited circuits (where the T80 hits the lower limit) will result in the charge level in the SAG mill dropping until its power draw matches the throughput limit dictated by the ball mill. It is important to realize that once the SAG mill charge level drops below the ball charge, it can no longer empty and the mill power draw will be incalculable and an error message will appear.
Circuits that operate at or near the transfer size limits should be less efficient than the default formulas will estimate. If you have a design that is consistently operating around the limits, then consider adding a contingency to inflate the specific energy consumption estimates to account for this poor grinding efficiency. Alternatively, if you are designing a new circuit then choose a different combination of SAG and ball mills that operates in a more reasonable transfer size range.
The rod mill oversize feed factor (EF4RM) in the Barratt ESAG equation is calculated using the greater of the sample's rod mill or crushing work index. The optimal feed size and EF4 are both calculated using whichever is greater.
The ball mill oversize feed factor (EF4BM) is always calculated with the ball mill work index. The optimal feed size for the EF4BM is always calculated using the rod mill work index.
The Easag RM value in the circuit configuration is used to specify which work index to use for a particular size (RM above this size or BM below it). The RM and BM work index values are frequently pretty similar, so the model won't be very sensitive to this configuration setting. If you have an ore with a large difference in RM and BM work index values, then you should pay close attention to which size this transition in hardness seems to manifest. The size where the shift occurs is where you specify the Easag RM value. A transition is sometimes observable in the particle size distributions of the feed and product material from the RM and BM tests – is there a "kink" in the size distribution in both the RM product and BM feed PSDs?
Recommended Usage
This model should be the upper end-member of the range of Bond/Barratt style models. It is useful when interpreting pilot plant results to determine where the pilot plant results fall relative to the spectrum of models. It can also be used as a conservative model for design work.
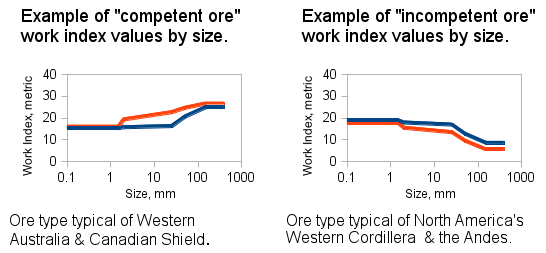
The Raw Bond/Barratt model is best used for highly competent ores, such as those found in Western Australia or the Canadian Shield, where the crushing work index is significantly greater than the rod mill and ball mill work index values. These ores also tend to not demonstrate a phantom cyclone effect which is more significant in the incompetent ore types.
Because this model does not include an internal phantom cyclone mechanism, it is customary to include an allowance for it in the Ball Mill contingency factor (in the circuit settings) by using a value of 0.95 (some fines in SAG product) to 0.85 (many fines in SAG product). If a SAG product does not include extra fines versus a standard size distribution, then use a value of 1.00 (typical of very hard Western Australian ores).
Because this model does not include an energy efficiency benefit due to pebble crushing, it may be necessary to apply a SAG contingency (in the circuit settings) value of less than one, for example: 0.95 would be a 5% energy benefit. The Minnovex CEET1 model and the Amnipro SGI model use a factor of this type. In their systems, SAG Contingency would be 1.00 for no pebble crushing, 0.85 for pebble crushing.
Default parameter values
- Maximum transfer size, µm = 6000
- Minimum transfer size, µm = 400 [Starkey et al. 2008]
- Hypothetical tertiary crusher product size, µm = 18850 [Barratt 1979]
- Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P80 and typical ball mill work index test F80).
![E_{SAG} = \left [ \left (
Wi_{C} \times \left ( \tfrac {10}{\sqrt{ P_{C} }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) +
Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ P_{R} }} - \tfrac {10}{\sqrt{ P_{C} }} \right ) \times EF_4^{RM} +
Wi_{BM} \times \left ( \tfrac {10}{\sqrt{110} } - \tfrac {10}{\sqrt{ P_{R} }} \right ) \times EF_4^{BM}
\right )\times 1.25 - Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ {110} }} - \tfrac {10}{\sqrt{ T_{80} }} \right ) \right ]
\times CF_{SAG}](/images/math/8/b/4/8b4892842c69af61c78f6564f75f347d.png)