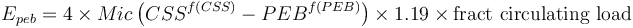Model:Morrell SS SAG
Contents
Morrell Mi (SMC) single-Stage SAG Mill Model
This is a SAG or AG mill model that estimates the specific energy consumption (ESAG) using the equations of Morrell (2004).
Testwork Required
- The SMC™ test, stored in the "DWT" testwork table (SMC is a Drop Weight Test).
- Bond ball mill work index. The method requires all the parameters of the ball mill work index test to be filled in:
- Ball mill Wi test closing screen size, umclosing, µm
- Ball mill Wi test product size, P80, µm
- Ball mill Wi test feed size, F80, µm
- Ball mill Wi grams per revolution at test conclusion, gpr
Required parameters
- F80, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
- P80, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
- Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
Optional parameters
- Description and Comment are optional text fields
- Maximum t/h limit is a t/h throughput above which a warning message is displayed (but does not actually limit the throughput).
- CFsag calibration factor, model tuning factor for EASAG
Formulae
The method is superficially similar to Bond (among other models), but with a variable exponent on size defined by:
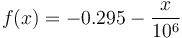
Where x is the particle 80% passing size in µm.
SAG with pebble crushing circuit: 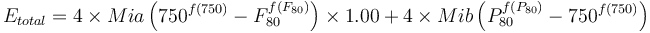 Morrell, 2004
Morrell, 2004
SAG with pebble crushing circuit: 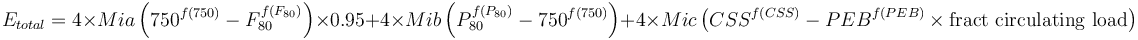 Morrell, 2004
Morrell, 2004
Circuits with a pebble crusher have an extra term to account for the pebble crusher specific energy, which requires an estimate of the pebble crusher F80 (PEB, the size of the pebbles as µm) and the pebble crusher product P80 (approximately the crusher's closed side setting as µm, CSS). The quantity of material passing through the pebble crusher is also required, expressed as a fraction of the fresh feed rate to the SAG circuit. Pebble crushers are expected to operate in open circuit, so the open circuit factor 1.19 applies.
For the purposes of simulations (and because the Epeb term tends to be small), the following conditions are assumed:
- fraction of circulating load = 0.15
- pebble crusher CSS (P80) = 12.5 mm
- pebble dimension (F80) = 35 mm
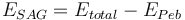
CFsag calibration factor
The CFsag factor is used to reflect the effect of pebble crushing on the overall circuit performance. This value is automatically selected if you leave this field blank in the model configuration settings.
- Base value, SAB circuit (no pebble crushing, ~6 inch SAG feed), CFsag = 1.00
- Pebble crushing, SABC circuit, CFsag = 0.95