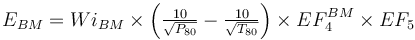Model:Bond RMBM Model
Bond/Rowland rod mill ball mill model
This is a rod mill feeding a ball mill model that estimates the specific energy consumption (ERM and EBM) using the Rowland interpretation of the classical Bond work index equation including Rowland efficiency factors.
There are two varieties of this model, one based on feed generated by closed-circuit crushing and other based on feed generated by open-circuit crushing.
Warning: do not mix sizes of rod mills, only have a single size of rod mill in the primary section. The estimation of Rowland EF6 factors requires rod mill dimensions, and only the first rod mill in the circuit is queried to calculate the EF6.
Testwork Required
Formulae
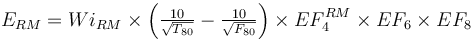
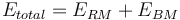
The rod mill oversize feed factor (EF4RM) is calculated using the greater of the sample's rod mill or crushing work index (which is usually the WiRM). The optimal feed size and EF4 are both calculated using whichever is greater.
![EF_4^{RM} =\left [ 1 + \left( \frac{ (0.907 \times Wi_{RM} - 7) }{ \left (\frac{F_{80} }{ T_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 16 000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]](/images/math/2/7/c/27cb6782d414da805410db603189ef54.png)
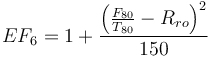
where,
Rro = 8 + 5 × (rod length) / (mill diam)
units aren't important as long as the mill diameter and rod length are expressed in the same units.
EF8 = 1.0 for rod mills fed by closed circuit crushing plants.
EF8 = 1.2 for rod mills fed by open circuit crushing plants.
Both the ball mill and rod mill work index values are used to compute EF4BM: The ball mill work index in the oversize feed factor component and the rod mill work index in the optimal feed size component.
![EF_4^{BM} =\left [ 1 + \left( \frac{(0.907 \times Wi_{BM} - 7) }{ \left (\frac{T_{80} }{ P_{80}} \right )} \right) \left ( {\frac{T_{80} }{ { 4000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]](/images/math/3/4/e/34ec5343663db3e292e9c0623a6b2f89.png)
where:
- F80, µm is the specified circuit feed size (crushing plant product)
- T80, µm is the transfer size that balances the power draw in rod & ball mill stages.
- P80, µm is the specified product size (hydrocyclone overflow)
Note that the EF3 factor is not used in these equations. Rowland describes omitting EF3 as a conservative design, adding a 'safety factor' to larger diameter mills.
Required parameters
- F80, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
- P80, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
- Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
Optional parameters
- Description and Comment are optional text fields
- Maximum t/h limit is a t/h throughput above which a warning message is displayed (but does not actually limit the throughput).
- T80 min and T80 min override the transfer size restrictions built into the model
- Ball mill work index adjustment used to adjust WiBM for different P80 sizes.
- coefficient (a), the fitted Hukki coefficient to the adjustment equation (enter as a positive number)
Secondary and tertiary crushers
The model assumes any secondary and/or tertiary crushing happens upstream of the rod mill. Crusher specific energy is not included in this model.
The choice of crushers and arrangement is normally based on volumetric flow and not on power draw. Use a crusher catalogue or another tool, like Metso's Bruno software, to determine the size and arrangement of the crushers ahead of the ball mill(s).