Ball mill work index adjustment
The Bond ball mill work index test requires the operator to select an appropriate screen size to "close" the test. The procedure states that the closing screen size should be such that the product size of the test is the same as the expected product size of the operating plant. If the tests were done at the wrong closing screen size, then a ball mill work index adjustment may be required.
The Morrell Mib value also requires an appropriate choice of screen, and it is usually more sensitive to variation in P80 than the Bond work index.
Contents
Laboratory program needed to perform adjustment
Adjustment procedure using the Josefin equation is conducted as follows:
- In the laboratory, select a series of samples, each suitable for performing three or more work index tests (probably 30 kg of sample is the practical minimum).
- Conduct a series of work index determinations on each sample, but vary the closing screen mesh. At minimum, test two different closing mesh sizes (the closing size you did the original tests at, and the closing size that matches your new desired P80). Three or four different mesh sizes are better.
- Calculate the Bond specific energy of each ball mill test, Eball = 10 × Wi (P80-0.5 - F80-0.5). If you are going to use Morrell equations, then also calculate the Morrell specific energy for each ball mill test, Eball = 4 × Mib (P80-0.295-P80×10^-6 - F80-0.295-F80×10^-6).
- Fit the specific energy results for all BM tests, Eball = K × P80-a. Use the power regression model or use logarithms to rearrange and solve for a and K using linear regression of the logarithms.
- If there is a clear discontinuity in the work index at a particular size, this probably indicates a hard grain size is being encountered in the test. If this grain size is between your original test P80 and the desired, P80, just continue with the procedure. If this grain size is above or below the size range of interest, then exclude those sizes and repeat the regression.
The precise method used to do the adjustment is based on Josephin & Doll (2018).
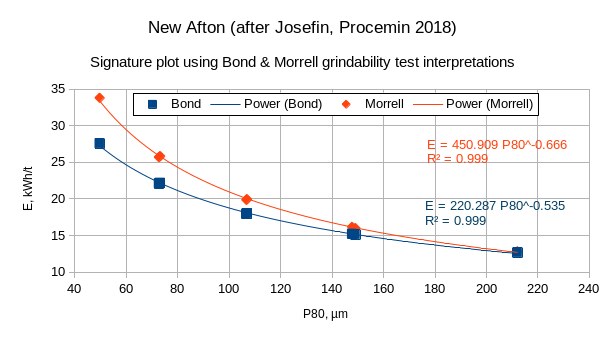
- Several Bond ball mill grindability tests were conducted using the New Afton ore sample. The Specific Energy Consumption (E) is computed for each test using both the methods of Bond and Morrell.
Example using the Josefin & Doll published signature plot:
- The exponent a for Bond equations is 0.535 and the exponent a for Morrell equations is 0.666. This is the value that is entered into the Circuit Configuration settings.
- The coefficient K for this sample is 220 for Bond models and 451 for Morrell models. This coefficient is not entered, the software automatically computes it when the a value is specified.
Ball mill work index adjustment
- Perform the laboratory program on a one or two representative samples to determine the Hukki Exponent (-a).
- Enter this (a) value (without the minus sign) into the Circuit Settings of a Bond specific energy model. The software will automatically adjust all compatible test results using this exponent.
Only samples where the F80, P80, and gpr values are entered into the project testwork database can be adjusted. Any sample that is missing any of these parameters will not be adjusted.
What the SAGMILLING.COM software does (Bond Wi version)
The laboratory ball mill work index result is read from the database (P80, P100, F80, and gpr; if multiple results exist with a particular sample name, then the averages of each parameter are used). The value K is determined for the sample, the parameter -a is read from the Circuit Settings, and the P80|adjusted is read from the simulation model (the P80 displayed at the top-left of the Flowsheet page, which might be different to the target P80 entered in the Circuit Settings).
- Compute K values for an individual grindability result:
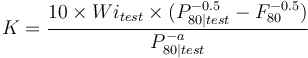
The Wiadjusted is computed using the equation below.
- The adjusted work index for an individual grindability result uses the K value:
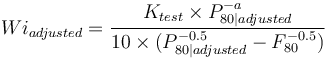
Morrell Mib adjustment
- Perform the laboratory program on a one or two representative samples to determine the Hukki Exponent (-a).
- Enter this (a) value (without the minus sign) into the Circuit Settings of a Bond specific energy model. The software will automatically adjust all compatible test results using this exponent.
Theory behind performing an adjustment
The Morrell Mi equations are in the form of Hukki's Conjecture, so the adjustment procedure is also valid for adjusting an Mib value to a different particle size if you have measured the ore's exponent a. It follow the similar process to the Wi correction where a Hukki exponent is determined in 3+ Bond ball mill grindability determinations using Morrell's equation for the specific energy term, then Hukki's equation is solved for constant K at the tests' P80 values

where 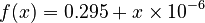
rearranging to solve for K (note the sign changes on the P exponent)
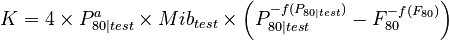
This K is assumed to be valid for all sizes within the calibration range of a Bond ball mill grindability test (P80 between about 70 µm and 350 µm).
To generate a synthetic Mib value for a different P80, do the adjustment using the Hukki equation with the K and a for your ore, then set the Morrell equation equal to that adjusted E value.
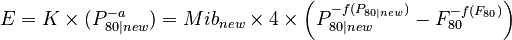
now rearrange for the new, adjusted, Mib value:
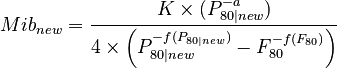
What the SAGMILLING.COM software does (Morrell Mi version)
The laboratory ball mill work index result is read from the database (P80, P100, F80, and gpr; if multiple results exist with a particular sample name, then the averages of each parameter are used). The value K is determined for the sample, the parameter -a is read from the Circuit Settings, and the P80|new is read from the simulation model (the P80 displayed at the top-left of the Flowsheet page, which might be different to the target P80 entered in the Circuit Settings). The Mibnew is computed using the equation above.
Comments
- Enter the exponent a into the Ball mill Wi adjust exponent (a) (drop the negative sign, a should always be positive when you enter it).
- The value of a is different if you are doing Bond modelling or Morrell modelling. Always measure the exponent a using the signature plot based on the model you intend to run (Bond or Morrell).
- This adjustment only applies to regular Bond ball mill grindability tests. The model will ignore the adjustment for any sample identified as a "modified ball mill test" (where the ModBWI is set to a non-zero number).
- If you want to manually compute the parameters of a synthetic sample using Josefin's equation and back-calculate the WiBM parameters to match, determine & enter:
- your desired P80 size for the sample,
- the P100 at your desired P80 (by interpolation),
- the Wi at your desired P80,
- enter the F80 observed in the test,
- then compute gpr from:
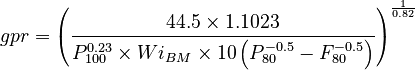
- If you want create a synthetic sample that gives both the interpolated WiBM and Mib, then enter
- the interpolated WiBM,
- P80|new,
- F80 observed in the test,
- interpolated P100, and then
- Compute & enter the gpr that gives the correct Mib value via this equation:
![gpr = \frac{18.18}{P_{100}^{0.295} (Mib|new) \left[ P_{80}^{-0.295-P_{80} \times 10^{-6}} - F_{80}^{-0.295-F_{80} \times 10^{-6}} \right]}](/images/math/9/d/4/9d4d0e918781f406cad272cd0df2dbd0.png)