Model:Bond/Barratt SABC Models
Contents
Bond/Barratt Specific Energy Consumption SABC Model
This is a SAG or AG mill plus ball mill model that estimates the overall circuit specific energy consumption using the classical Bond work index equation for multi-stage crushing and single-stage ball milling (Essbm) including Rowland efficiency factors. The circuit Etotal is equal to the Essbm plus an inefficiency factor (CF) related to the difference in grinding efficiency of the two types of circuits. The SAG mill specific energy consumption (ESAG) is calculated using the 1979 Barratt equation and the ball mill specific energy consumption (Ebm)
This model includes a phantom cyclone effect in the equations due to the ball mill being calculated by difference and not being calculated by the normal Bond equation. The resultant operating work index of the ball mill will vary according to the ratio of the ball mill, rod mill and crushing work index values and is in the range of 80% of the measured ball mill work index value.
Testwork Required
Required parameters
- F80, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
- P80, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
- Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
- Ball mill Operating strategy when circuit is SAG-limited (note, fixed speed can only be vary P80)
Optional parameters
- Description and Comment are optional text fields
- Maximum t/h limit is a t/h throughput limit above which the mills will turn down by, for example, grinding out.
- T80 min and T80 min override the transfer size restrictions built into the model
- Ball mill work index adjustment used to adjust WiBM for different P80 sizes.
- exponent (a), the fitted Hukki exponent to the adjustment equation (enter as a positive number)
- Essbm calibration factor (CF), model tuning factor for Etotal
- Easag crushing circuit product, model tuning factor that dictates where the Barratt Easag equation switches from using the crushing Wi to the rod mill Wi
- Easag RM circuit product, model tuning factor that dictates where the Barratt Easag equation switches from using the rod mill Wi to the ball mill Wi
- Essbm crushing circuit product, model tuning factor that dictates where the Bond Essbm equation (the basis for the Barratt Etotal equation) switches from using the crushing Wi to the rod mill Wi
Formulae
where
- Pcssbm is the calibration value entered for "Essbm crushing circuit product" (default: 9400)
- Prm is the calibration value entered for "Easag RM circuit product" (default: 2100)
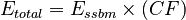
where
- PC is the calibration value entered for "Easag crushing circuit product" (default: 18850)
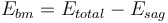
As with most models, the power split between the SAG and ball mills is evaluated and the transfer size (T80) necessary to balance the power draw between the two stages is estimated. If that transfer size is within the specified limits, then the calculation proceeds to calculate the ESAG and Ebm using that transfer size. If the transfer size to balance the power is outside the specified limits, then the transfer size size is forced to the limit and the ESAG and Ebm values are then calculated. SAG-limited circuits (where the T80 hits the upper limit) will result in the ball mill over-grinding unless the ball mill speed is reduced to control the grind size (in the case of a variable speed mill). Ball-limited circuits (where the T80 hits the lower limit) will result in the charge level in the SAG mill dropping until its power draw matches the throughput limit dictated by the ball mill. It is important to realize that once the SAG mill charge level drops to be equal to the ball charge, the model will be operating "out of range" and the predictions will not be valid.
Circuits that operate at or near the transfer size limits should be less efficient than the default formulas will estimate. If you have a design that is consistently operating around the limits, then consider adding a contingency to inflate the specific energy consumption estimates to account for this poor grinding efficiency. Alternatively, if you are designing a new circuit then choose a different combination of SAG and ball mills that operates in a more reasonable transfer size range.
The optimum feed size for the rod mill oversize feed factor (EF4RM) in the Barratt ESAG equation is calculated using the greater of the sample's rod mill or crushing work index.
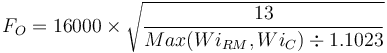
The EF4RM is calculated greater of the crushing work index or the rod mill work index.
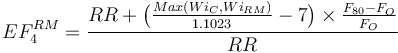
The ball mill oversize feed factor (EF4BM) is always calculated with the rod mill work index for the optimum feed size and the ball mill work index for EF4BM.
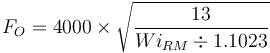
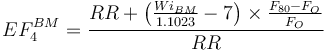
The model assumes that the calculated value of Essbm + the specified contingency is greater than the sum of Esag + Epeb; otherwise Ebm will be negative. The model does a check to see if Ebm calculated is negative (or close to zero) and, if so, will substitute the Raw Bond Model equation estimate for Ebm.
Recommended Usage
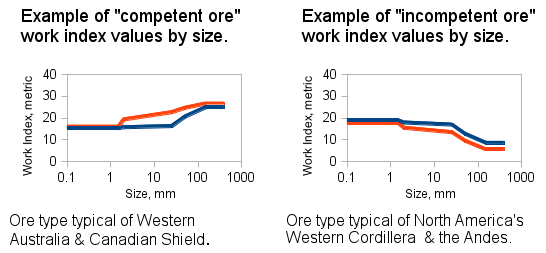
This model should be the lower end-member of the range of Bond/Barratt style models. It is useful when interpreting pilot plant results to determine where the pilot plant results fall relative to the spectrum of models. It can be used as a realistic model for design work in softer ore types like copper porphyries. The Optimized Bond/Barratt model is best used for low competency ores, such as those found in the Western Cordillera of North America or the Andes, where the impact crushing work index is similar to, or less than the rod mill and ball mill work index values. These ores tend to demonstrate a phantom cyclone effect.
Discussion, pebble crushing
The pebble crusher is assumed to be part of the SAG mill for the purposes of this calculation. Epeb is calculated as the power drawn by the pebble crusher divided by the circuit throughput. This Epeb is then deducted from Esag.
The total circuit specific energy consumption is generally higher when no pebble crusher is present in a circuit. The rule of thumb is apply the CF value of 1.15 for SAB circuits (5% higher overall specific energy consumption) Bennett, Dobby & Kosick, SAG 2001. Published data from Cadia confirms a 5% difference in throughput (and therefore, specific energy) when the pebble crusher is fully utilized.Hart, Valery, Clements, Reed, Song & Dunne, SAG 2001.
Discussion, Rowland EF factors
The model is only interested in the EF factors that are properties of the rock, namely the coarse feed EF4 factor and the fine product EF5 factor. The EF factors that correspond to machine characteristics are not included (EF1, EF2, EF3, EF6, EF7 and EF8) as they are intended to capture the inefficiency of certain types of milling circuits. The assumption in this model is that the Essbm is the "maximum efficiency" possible for a grinding circuit, to which we apply an empirical adjustment for SAG milling (Cf) which encapsulates any other EF factors in a form suitable for a SAG process.
Model defaults
- Maximum T80, µm = 6000
- Minimum T80, µm = 400
- PC for Essbm= 9400
- PC for Easag= 18850
- PR= 2100
- CF = 1.10
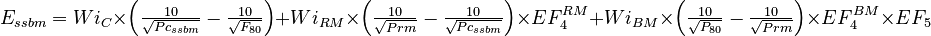
![\begin{align}
E_{SAG} = \Big[ & Wi_{C} \times \left ( \tfrac {10}{\sqrt{ P_{C} }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) + Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ P_{R} }} - \tfrac {10}{\sqrt{ P_{C} }} \right ) \times EF_4^{RM} \\
& + Wi_{BM} \times \left ( \tfrac {10}{\sqrt{110} } - \tfrac {10}{\sqrt{ P_{R} }} \right ) \times EF_4^{BM} \Big] \times 1.25 - Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ {110} }} - \tfrac {10}{\sqrt{ T_{80} }} \right )
\end{align}](/images/math/c/e/5/ce54d618ebdca7ae6f6579b12a6e42a3.png)