Model:Bond/Barratt SAB Model

Bond/Barratt Specific Energy SAB Consumption Model

This is a SAG or AG mill plus ball mill model that estimates the overall circuit specific energy consumption using the classical Bond work index equation for multi-stage crushing and single-stage ball milling (E_ssbm) including Rowland efficiency factors. The circuit E_total is equal to the E_ssbm plus an inefficiency/contingency factor (CF) related to the difference in grinding efficiency of the two types of circuits. The SAG mill specific energy consumption (E_SAG) is calculated using the 1979 Barratt equation and the ball mill specific energy consumption (E_bm)

This model includes a phantom cyclone effect in the equations due to the ball mill being calculated by difference and not being calculated by the normal Bond equation. The resultant operating work index of the ball mill will vary according to the ratio of the ball mill, rod mill and crushing work index values and for an Andean copper porphyry is typically in the range of 80% of the measured ball mill work index value.

Testwork Required

• Bond ball mill work index
• Bond rod mill work index
• Bond crushing (low-energy impact) work index

Required parameters

• F₈₀, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
• P₈₀, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
• Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
• Ball mill Operating strategy when circuit is SAG-limited (note, fixed speed can only be vary P₈₀)

Optional parameters

• Description and Comment are optional text fields
• Maximum t/h limit is a t/h throughput limit above which the mills will turn down by, for example, grinding out.
• T₈₀ min and T₈₀ min override the transfer size restrictions built into the model
• Ball mill work index adjustment used to adjust Wi_BM for different P₈₀ sizes.
  • coefficient (a), the fitted Hukki coefficient to the adjustment equation (enter as a positive number)
• Essbm calibration factor, model tuning factor for E_total

Formulae

$E_{ssbm} = Wi_{C} \times \left ( \tfrac {10}{\sqrt{ 9400 }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) + Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ 2100 }} - \tfrac {10}{\sqrt{ 9400 }} \right )\times EF_4^{RM} + Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ P_{80} }} - \tfrac {10}{\sqrt{ 2100 }} \right ) \times EF_4^{BM} \times EF_5$

$E_{total} = E_{ssbm} \times (1+CF)$

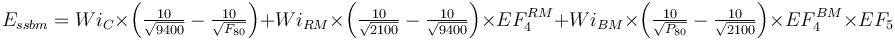
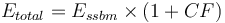
$\begin{align} E_{SAG} = \Big[ & Wi_{C} \times \left ( \tfrac {10}{\sqrt{ P_{C} }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) + Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ P_{R} }} - \tfrac {10}{\sqrt{ P_{C} }} \right ) \times EF_4^{RM} \\ & + Wi_{BM} \times \left ( \tfrac {10}{\sqrt{110} } - \tfrac {10}{\sqrt{ P_{R} }} \right ) \times EF_4^{BM} \Big] \times 1.25 - Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ {110} }} - \tfrac {10}{\sqrt{ T_{80} }} \right ) \end{align}$

$E_{bm} = E_{total} - E_{asag}$

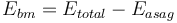
Discussions

Refer to the discussions in the Bond/Barratt SABC circuit model for background on the transfer size and the use of the Rowland efficiency factors (EF4 & EF5).

Model defaults

• Maximum T₈₀, µm = 5000
• Minimum T₈₀, µm = 400
• P_C for Essbm= 9400
• P_C for Easag= 18850
• P_R= 2100
• CF = 0.15