Difference between revisions of "Testwork: Bond ball mill work index"
(→Test Outputs) |
(→Testwork: Bond Ball Mill Work Index) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
[[Category:Amelunxen SGI Model]] |
[[Category:Amelunxen SGI Model]] |
||
==Testwork: Bond Ball Mill Work Index== |
==Testwork: Bond Ball Mill Work Index== |
||
| − | {{Test|name=Bond Ball Mill Work Index|Abrev=Wi<sub>BM</sub>|Alt=BWI|F80= |
+ | {{Test|name=Bond Ball Mill Work Index|Abrev=Wi<sub>BM</sub>|Alt=BWI|F80=2440 µm|P80=75-300 µm|Models=Bond models, SGI, Morrell Mi}} |
The Bond ball mill work index is one of the most commonly used grindability tests in mining, and is often referred to as ''the Bond work index''. |
The Bond ball mill work index is one of the most commonly used grindability tests in mining, and is often referred to as ''the Bond work index''. |
||
| Line 34: | Line 34: | ||
<math> Wi_{BM} = \frac{1.1023 \times 44.5}{P_{100}^{0.23} \times gpr^{0.82} \times (\frac{10}{\sqrt{P_{80}}} - \frac{10}{\sqrt{F_{80}}})}</math> |
<math> Wi_{BM} = \frac{1.1023 \times 44.5}{P_{100}^{0.23} \times gpr^{0.82} \times (\frac{10}{\sqrt{P_{80}}} - \frac{10}{\sqrt{F_{80}}})}</math> |
||
| − | |||
| − | NI43-101 reports often provide P<sub>100</sub> and the work index. To estimate the other parameters, you can assume: |
||
| − | * the P<sub>80</sub> is 0.92 × (P<sub>100</sub>, µm)<sup>0.96</sup> |
||
| − | (https://www.linkedin.com/posts/alex-doll-66b57465_workindex-comminution-grinding-activity-6873690907527532544-u6DD) |
||
| − | * assume the F<sub>80</sub> is 2440 µm |
||
| − | |||
| − | The grams per revolution can be computed by rearranging Bond's laboratory equation: |
||
| − | |||
| − | <math> gpr = \left[ \frac{1.1023 \times 44.5}{P_{100}^{0.23} \times Wi_{BM} \times (\frac{10}{\sqrt{P_{80}}} - \frac{10}{\sqrt{F_{80}}})} \right]^\frac{1}{0.82} </math> |
||
===Derived values composed from Wi<sub>BM</sub> results=== |
===Derived values composed from Wi<sub>BM</sub> results=== |
||
| Line 49: | Line 40: | ||
** This value is used in the [[:Category:SMC Model|Morrell Mi models]]. |
** This value is used in the [[:Category:SMC Model|Morrell Mi models]]. |
||
** <math>Mib = \frac{18.18}{P_{100}^{0.295} × (gpr) \left [ P_{80}^{f(P_{80})} - F_{80}^{f(F_{80})} \right ]} </math> kWh/t |
** <math>Mib = \frac{18.18}{P_{100}^{0.295} × (gpr) \left [ P_{80}^{f(P_{80})} - F_{80}^{f(F_{80})} \right ]} </math> kWh/t |
||
| + | ** where: f(''x'') = -0.293 - ''x''/10⁶ |
||
* ''Levin B'' parameter is calculated for a sample if the following are available: '''umClosing''', '''F80''', '''P80''', '''gpr''', '''fdpassing'''. |
* ''Levin B'' parameter is calculated for a sample if the following are available: '''umClosing''', '''F80''', '''P80''', '''gpr''', '''fdpassing'''. |
||
| − | ** Units of the Levin B are mWh per revolution of a standard Bond grindability ball mill (mWh/rev). Watch out as this metric is also given as kWh/rev in literature. |
+ | ** Units of the Levin B are mWh per revolution of a standard Bond grindability ball mill (mWh/rev). Watch out, as this metric is also given as kWh/rev in literature. |
** This value is not used in any computations, but can be used in external calculation such as [https://sagmilling.com/articles/37/view/2020%20CMP%20-%20Alex%20Doll.pdf?s=1 Functional Performance]. |
** This value is not used in any computations, but can be used in external calculation such as [https://sagmilling.com/articles/37/view/2020%20CMP%20-%20Alex%20Doll.pdf?s=1 Functional Performance]. |
||
** <math>B = \frac{4900 × (gpr)^{0.18}}{P_{100}^{0.23} (100 - Fd%passing)}</math> mWh/rev |
** <math>B = \frac{4900 × (gpr)^{0.18}}{P_{100}^{0.23} (100 - Fd%passing)}</math> mWh/rev |
||
| Line 66: | Line 58: | ||
=== Corrections and adjustments === |
=== Corrections and adjustments === |
||
| + | |||
| + | '''Estimate of P<sub>80</sub> when P<sub>100</sub> is known''' |
||
| + | |||
| + | (Source https://www.linkedin.com/posts/alex-doll-66b57465_workindex-comminution-grinding-activity-6873690907527532544-u6DD) |
||
| + | |||
The P<sub>80</sub> of a ball mill work index test can be estimated if the P<sub>100</sub> is know based on this equation: |
The P<sub>80</sub> of a ball mill work index test can be estimated if the P<sub>100</sub> is know based on this equation: |
||
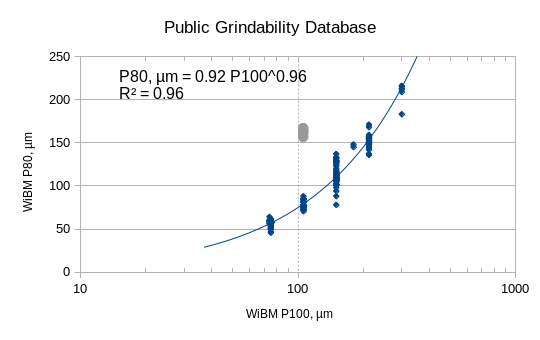
<math>P_{80}=0.92 × (P_{100})^{0.96}</math> |
<math>P_{80}=0.92 × (P_{100})^{0.96}</math> |
||
[[File:P80_P100-powermodel.png]] |
[[File:P80_P100-powermodel.png]] |
||
| + | |||
| + | '''Estimate grams per revolution when only P100 is known''' |
||
| + | |||
| + | NI43-101 reports often provide P<sub>100</sub> and the work index. To estimate the other parameters, you can assume: |
||
| + | * the P<sub>80</sub> is 0.92 × (P<sub>100</sub>, µm)<sup>0.96</sup> |
||
| + | * assume the F<sub>80</sub> is 2440 µm (see [[https://www.researchgate.net/publication/363350623_A_new_methodology_to_obtain_a_corrected_Bond_ball_mill_work_index_valid_with_non-standard_feed_size Nikolić, Doll, & Trumić (2022)]]) |
||
| + | |||
| + | The grams per revolution can be computed by rearranging Bond's laboratory equation: |
||
| + | |||
| + | <math> gpr = \left[ \frac{1.1023 \times 44.5}{P_{100}^{0.23} \times Wi_{BM} \times (\frac{10}{\sqrt{P_{80}}} - \frac{10}{\sqrt{F_{80}}})} \right]^\frac{1}{0.82} </math> |
||
| + | |||
To adjust a ball mill grindability test work index or Mib value to a different P<sub>80</sub> basis, use the [[Ball mill work index adjustment]] method of Josefin & Doll. |
To adjust a ball mill grindability test work index or Mib value to a different P<sub>80</sub> basis, use the [[Ball mill work index adjustment]] method of Josefin & Doll. |
||
| + | |||
| + | '''Correct for 'non standard' feed size''' |
||
| + | |||
| + | If the ball mill test feed material was too small for the stage crushing to make a normal F80, then the correction from ''Nikolić, Doll, & Trumić (2022)'' [[https://www.researchgate.net/publication/363350623_A_new_methodology_to_obtain_a_corrected_Bond_ball_mill_work_index_valid_with_non-standard_feed_size A new methodology to obtain a corrected Bond ball mill work index valid with non-standard feed size]] may be applied. The method is also described in Procemin 2022 paper [[https://www.researchgate.net/publication/372393426_Secrets_of_the_Bond_Ball_mill_grindability_test Secrets of the Bond Ball Mill Grindability Test]] |
||
| + | |||
| + | === Computing Mib from incomplete Ball Mill Work Index data === |
||
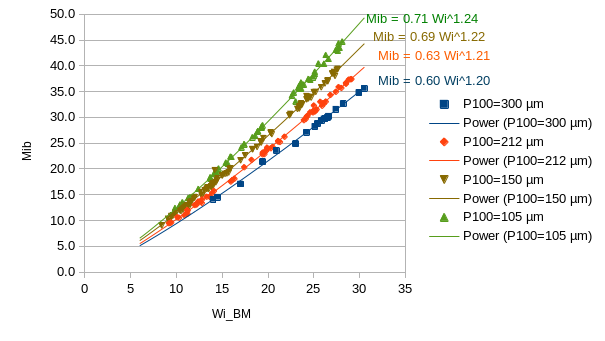
| + | Use this nomograph to compute an Mib from a ball mill work index if you know the P100 size that the test should be run at. |
||
| + | |||
| + | [[File:MibFromWiBM byP100.png]] |
||
Latest revision as of 14:31, 3 July 2024
Contents
Testwork: Bond Ball Mill Work Index
| Test name | ||||
| Bond Ball Mill Work Index | ||||
| ||||
| ||||
| Models | ||||
| Bond models, SGI, Morrell Mi |
The Bond ball mill work index is one of the most commonly used grindability tests in mining, and is often referred to as the Bond work index.
The test is a 'locked-cycle' test where ground product is removed from test cycles and replaced by fresh feed. The test much achieve a steady-state before completion.
Sample Requirements
The test requires about 8 kg of material. Although it can work on feed as fine as 2.5 mm, it is best to send material to the testing laboratory that is nominally at least 8 mm (including the natural fines that are part of the sample). The laboratories have a standard way of reducing the coarse material to the (roughly) 2.5 mm size used to feed the test that will not introduce excessive fines.
Test Inputs
It is necessary for the engineer to specify the desired product size of the test so that the laboratory can choose the appropriate closing mesh screen for conducting the test. This product size is typically the feed size to flotation or leaching. Example product sizes are 200 µm for copper porphyries (select a 212 µm screen), 100 µm for gold cyanidation (select a 150 µm or 125 µm closing screen) or 75 µm for complex sulphides (select a 105 µm screen).
Test Outputs
The laboratory will report the following information:
- umClosing: The closing mesh size the test was run at, also called P100 or P1. Convert to µm, if needed, before entering into the database.
- F80: Sample feed size in µm (and usually will provide a particle size distribution)
- P80: Sample finished product size in µm (and usually will provide a particle size distribution)
- gpr: The average grams per revolution of the last three cycles (sometimes is labelled GPB)
- fdpassing: The percentage (0-100) of the feed that already passes the closing screen size
- WiBM: The calculated work index (SAGMILLING.COM uses only metric units; if the laboratory reported work index in "short ton" units, multiply that value by 1.1023 and enter the result).
When entering results into the SAGMILLING.COM database table, the following extra fields are available:
- ModBWI: is this test modified from the original Bond protocol? An open-circuit Minnovex ModBWI test or a SAGDesign ball mill work index with non-standard feed would be entered as "true" (or "1" in a batch upload of test results).
- synthetic indicates whether this is a real test result, or just a synthetic one that should only be used for modelling. If this column contains a value of '1' (boolean=true) for a test, then that test is understood to not be a real test result and is therefore not shown on the testwork comparison charts. Synthetic values are available when running circuit model simulations and do show up in the list of model results.
The computation of a Bond ball mill work index was empirically calibrated by Fred Bond using a short ton basis. The modern (metric tonne) basis is the following equation:

Derived values composed from WiBM results
- Morrell Mib value is calculated for a sample if the following are available: umClosing, F80, P80, gpr.
- Units are kWh/t based on Morrell's empirical calibration.
- This value is used in the Morrell Mi models.
![Mib = \frac{18.18}{P_{100}^{0.295} × (gpr) \left [ P_{80}^{f(P_{80})} - F_{80}^{f(F_{80})} \right ]}](/images/math/b/b/1/bb10abf4ea979de37ca4e68e8b29f614.png) kWh/t
kWh/t- where: f(x) = -0.293 - x/10⁶
- Levin B parameter is calculated for a sample if the following are available: umClosing, F80, P80, gpr, fdpassing.
- Units of the Levin B are mWh per revolution of a standard Bond grindability ball mill (mWh/rev). Watch out, as this metric is also given as kWh/rev in literature.
- This value is not used in any computations, but can be used in external calculation such as Functional Performance.
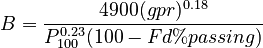 mWh/rev
mWh/rev
Modelling
Ball mill work index is used in several SAGMILLING.COM circuit models, including:
- Bond/Barratt specific energy consumption circuit model.
- Bond/Rowland rod mill & ball mill specific energy consumption circuit model.
- Amelunxen SGI SAG and ball mill circuit model.
- Morrell SMC (Mib) SAG and ball mill circuit model (uses the umclosing, F80, P80, and gpr values to calculate Mib).
It is also used in the CEET2 model (distributed by SGS) and is commonly used by people running the JK SimMet population balance model (distributed by JK Tech).
The work index is used to calculate the energy requirement to grind rocks in the fine size range, below 2.5 mm into the range of a few hundreds of micrometres. Heterogeneous ore types typically are sensitive to the product size of the test, and the work index value changes if the test is performed to a coarser or finer product. Always specify the desired product size of the test to the laboratory, or conduct a Ball mill work index adjustment procedure to determine the effect of changing the product size on work index.
Corrections and adjustments
Estimate of P80 when P100 is known
The P80 of a ball mill work index test can be estimated if the P100 is know based on this equation:
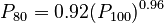
Estimate grams per revolution when only P100 is known
NI43-101 reports often provide P100 and the work index. To estimate the other parameters, you can assume:
- the P80 is 0.92 × (P100, µm)0.96
- assume the F80 is 2440 µm (see [Nikolić, Doll, & Trumić (2022)])
The grams per revolution can be computed by rearranging Bond's laboratory equation:
![gpr = \left[ \frac{1.1023 \times 44.5}{P_{100}^{0.23} \times Wi_{BM} \times (\frac{10}{\sqrt{P_{80}}} - \frac{10}{\sqrt{F_{80}}})} \right]^\frac{1}{0.82}](/images/math/8/f/3/8f35070bb3589e376e86db30eabc7c95.png)
To adjust a ball mill grindability test work index or Mib value to a different P80 basis, use the Ball mill work index adjustment method of Josefin & Doll.
Correct for 'non standard' feed size
If the ball mill test feed material was too small for the stage crushing to make a normal F80, then the correction from Nikolić, Doll, & Trumić (2022) [A new methodology to obtain a corrected Bond ball mill work index valid with non-standard feed size] may be applied. The method is also described in Procemin 2022 paper [Secrets of the Bond Ball Mill Grindability Test]
Computing Mib from incomplete Ball Mill Work Index data
Use this nomograph to compute an Mib from a ball mill work index if you know the P100 size that the test should be run at.