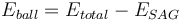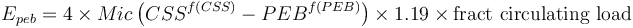Model:Morrell Mi SMC SAG
Contents
Morrell Mi (SMC) SAG & ball mill Model
This is a SAG or AG mill plus ball mill model that estimates the specific energy consumption (ESAG) using the equations of Morrell (2004).
Testwork Required
- The SMC™ test, stored in the "DWT" testwork table (SMC is a Drop Weight Test).
- Bond ball mill work index. The method requires all the following elements of the ball mill work index test to be filled in:
- Ball mill Wi test closing screen size, umclosing, µm
- Ball mill Wi test product size, P80, µm
- Ball mill Wi test feed size, F80, µm
- Ball mill Wi grams per revolution at test conclusion, gpr
Required parameters
- F80, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
- P80, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
- Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
- Ball mill Operating strategy when circuit is SAG-limited (note, fixed speed ball mills can only be vary P80)
Optional parameters
- Description and Comment are optional text fields
- Maximum t/h limit is a t/h throughput above which the SAG and ball mills will turn down by, for example, grinding out.
- T80 min and T80 min override the transfer size restrictions built into the model
- Ball mill work index adjustment used to adjust WiBM for different P80 sizes.
- coefficient (a), the fitted coefficient to the adjustment equation
- CFball calibration factor, model tuning factor for "W_b" fine component of Etotal
- CFsag calibration factor, model tuning factor for EASAG and "W_a" coarse component of Etotal
(raw E gets multiplied by these calibration factors, so E > 1 decreases tonnage; E < 1 increases tonnage)
Formulae
The method is superficially similar to Bond (among other models), but with a variable exponent on size defined by:
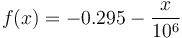
Where x is the particle 80% passing size in µm.
SAB circuit: 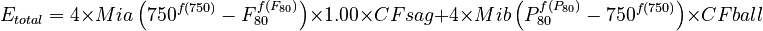 Morrell, 2004
Morrell, 2004
SABC circuit: 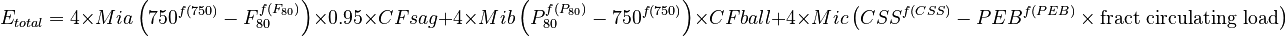 Morrell, 2004
Morrell, 2004
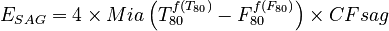 based on Doll 2013, but note Morrell, 2011
based on Doll 2013, but note Morrell, 2011
Circuits with a pebble crusher have an extra term to account for the pebble crusher specific energy, which requires an estimate of the pebble crusher F80 (PEB, the size of the pebbles as µm) and the pebble crusher product P80 (approximately the crusher's closed side setting as µm, CSS). The quantity of material passing through the pebble crusher is also required, expressed as a fraction of the fresh feed rate to the SAG circuit. Pebble crushers are expected to operate in open circuit, so the open circuit factor 1.19 applies.
For the purposes of simulations (and because the Epeb term tends to be small), the following conditions are assumed:
- fraction of circulating load = 0.15
- pebble crusher CSS (P80) = 12.5 mm
- pebble dimension (F80) = 35 mm
CFsag calibration factor
The CFsag factor is used to reflect the effect of pebble crushing on the overall circuit performance. This value is automatically selected if you leave this field blank in the model configuration settings.
- Base value, SAB circuit (no pebble crushing, ~6 inch SAG feed), CFsag = 1.00
- Pebble crushing, SABC circuit, CFsag = 0.95
Transfer size
Morrell specifically discourages use of transfer size in calculations such as those in SAGMILLING.COM for a variety of reasons (see discussion in Morrell, SAG 2011). Unfortunately, the alternative method proposed by Morrell is an equation that requires pre-selected mill sizes and a series of unpublished calibration factors. A calibration attempt by Paul Díaz (Procemin, 2015) shows wildly different fitted parameters for different Chilean operating mills. Morrell's alternative method is not practical for the calculations in SAGMILLING.COM (at least, not yet), so a transfer size approach is used instead.
The modelled transfer sizes are "Bond-compatible" and not similar to what would be measured directly in a plant survey. Plant survey results would need to be subjected to a phantom cyclone calculation before they are comparable to the model predictions.