Difference between revisions of "Model:Bond/Barratt SS SAG"
(Created page with "Category:Models Category:Specific Energy Models Category: Bond/Barratt Model == Bond/Barratt Specific Energy Consumption Single-Stage SAG Model == This is a SAG o...") |
(→Optional parameters) |
||
| Line 20: | Line 20: | ||
* '''Maximum t/h limit''' is a t/h throughput above which a warning message is displayed (but does not actually limit the throughput). |
* '''Maximum t/h limit''' is a t/h throughput above which a warning message is displayed (but does not actually limit the throughput). |
||
* [[Ball mill work index adjustment]] used to adjust Wi<sub>BM</sub> for different P<sub>80</sub> sizes. |
* [[Ball mill work index adjustment]] used to adjust Wi<sub>BM</sub> for different P<sub>80</sub> sizes. |
||
| − | ** '''coefficient (a)''', the fitted coefficient to the adjustment equation |
+ | ** '''coefficient (a)''', the fitted Hukki coefficient to the adjustment equation (enter as a positive number) |
| − | ** '''exponent (b)''', the fitted exponent to the adjustment equation |
||
* '''(calibration) Easag crushing circuit product, µm''', model tuning factor for that adjusts the relative weight of the Wi<sub>C</sub> and Wi<sub>RM</sub> |
* '''(calibration) Easag crushing circuit product, µm''', model tuning factor for that adjusts the relative weight of the Wi<sub>C</sub> and Wi<sub>RM</sub> |
||
* '''(calibration) Easag RM circuit product, µm :''', model tuning factor for that adjusts the relative weight of the Wi<sub>RM</sub> and Wi<sub>BM</sub> |
* '''(calibration) Easag RM circuit product, µm :''', model tuning factor for that adjusts the relative weight of the Wi<sub>RM</sub> and Wi<sub>BM</sub> |
||
* '''CFsag Calibration Factor''', is a manual adjustment to the model prediction. This value is multiplied by the prediction, so 1.0 means use the predicted value, 1.5 means use 50% more than the predicted value. |
* '''CFsag Calibration Factor''', is a manual adjustment to the model prediction. This value is multiplied by the prediction, so 1.0 means use the predicted value, 1.5 means use 50% more than the predicted value. |
||
| − | |||
===Formulae=== |
===Formulae=== |
||
Revision as of 19:48, 22 March 2020
Contents
Bond/Barratt Specific Energy Consumption Single-Stage SAG Model
This is a SAG or AG mill plus ball mill model that estimates the SAG mill specific energy consumption (ESAG) using the 1979 Barratt equation.
Testwork Required
Required parameters
- F80, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
- P80, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
- Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
Optional parameters
- Description and Comment are optional text fields
- Maximum t/h limit is a t/h throughput above which a warning message is displayed (but does not actually limit the throughput).
- Ball mill work index adjustment used to adjust WiBM for different P80 sizes.
- coefficient (a), the fitted Hukki coefficient to the adjustment equation (enter as a positive number)
- (calibration) Easag crushing circuit product, µm, model tuning factor for that adjusts the relative weight of the WiC and WiRM
- (calibration) Easag RM circuit product, µm :, model tuning factor for that adjusts the relative weight of the WiRM and WiBM
- CFsag Calibration Factor, is a manual adjustment to the model prediction. This value is multiplied by the prediction, so 1.0 means use the predicted value, 1.5 means use 50% more than the predicted value.
Formulae
The optimum feed size for the rod mill oversize feed factor (EF4RM) in the Barratt ESAG equation is calculated using the greater of the sample's rod mill or crushing work index.
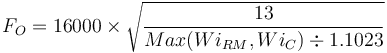
The EF4RM is calculated greater of the crushing work index or the rod mill work index.
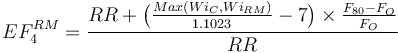
The ball mill oversize feed factor (EF4BM) is always calculated with the rod mill work index for the optimum feed size and the ball mill work index for EF4BM.
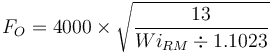
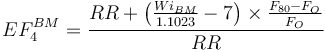
Recommended Usage
Discussion, pebble crushing
Barratt's equation did not consider pebble crushing; the practise was not common when his equation was being calibrated. Any pebble crusher is assumed to be part of the SAG mill for the purposes of this calculation and is assumed to operate at the same efficiency as the SAG mill itself. If you wish to model an improved SAG energy consumption due to pebble crushing, adjust the CFsag Calibration Factor to, for example, 0.95 for an assumed 5% benefit.
Discussion, Rowland EF factors
The model is only interested in the EF factors that are properties of the rock, namely the coarse feed EF4 factor and the fine product EF5 factor. The EF factors that correspond to machine characteristics are not included (EF1, EF2, EF3, EF6, EF7 and EF8) as they are intended to capture the inefficiency of certain types of milling circuits. The assumption in this model is that the Essbm is the "maximum efficiency" possible for a grinding circuit, to which we apply an empirical adjustment for SAG milling (Cf) which encapsulates any other EF factors in a form suitable for a SAG process.
Model defaults
- (calibration) Easag crushing circuit product, µm= 9400
- (calibration) Easag RM circuit product, µm= 2100
- CFsag Calibration Factor = 0.10
![\begin{align}
E_{SAG} = \Big[ & Wi_{C} \times \left ( \tfrac {10}{\sqrt{ P_{C} }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) + Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ P_{R} }} - \tfrac {10}{\sqrt{ P_{C} }} \right ) \times EF_4^{RM} \\
& + Wi_{BM} \times \left ( \tfrac {10}{\sqrt{110} } - \tfrac {10}{\sqrt{ P_{R} }} \right ) \times EF_4^{BM} \Big] \times 1.25 - Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ {110} }} - \tfrac {10}{\sqrt{ T_{80} }} \right )
\end{align}](/images/math/c/e/5/ce54d618ebdca7ae6f6579b12a6e42a3.png)