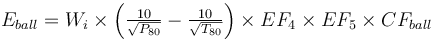Model:Raw Bond/Barratt SAB & SABC Model

Raw Bond Model

This is a SAG or AG mill plus ball mill model that estimates the specific energy consumption (E_SAG) using the 1979 Barratt equation and the classical Bond work index equation including Rowland efficiency factors. The model allows a manual calibration factor on both equations (CF_SAG and CF_ball, respectively).

This formula usually gives higher total circuit specific energy consumption estimates than the other Bond/Barratt models. This is largely due to the absence of a phantom cyclone effect in the equations.

$E_{SAG} = \left [ \left ( Wi_{C} \times \left ( \tfrac {10}{\sqrt{ P_{C} }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) + Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ P_{R} }} - \tfrac {10}{\sqrt{ P_{C} }} \right ) \times EF_4^{RM} + Wi_{BM} \times \left ( \tfrac {10}{\sqrt{110} } - \tfrac {10}{\sqrt{ P_{R} }} \right ) \times EF_4^{BM} \right )\times 1.25 - Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ {110} }} - \tfrac {10}{\sqrt{ T_{80} }} \right ) \right ] \times CF_{SAG}$ ^{Barratt, 1989}

$E_{ball} = W_i \times \left ( \tfrac {10}{\sqrt{ P_{80} }} - \tfrac {10}{\sqrt{ T_{80} }} \right ) \times EF_4 \times EF_5 \times CF_{ball}$^{Rowland, 2006}

$E_{total} = E_{SAG} + E_{ball}$

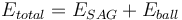
As with most models, the power split between the SAG and ball mills is evaluated and the transfer size (T₈₀) necessary to balance the power draw between the two stages is estimated. If that transfer size is within the specified limits, then the calculation proceeds to calculate the E_SAG and E_ball using that transfer size. If the transfer size to balance the power is outside the specified limits, then the transfer size size is forced to the limit and the E_SAG and E_ball values are then recalculated. SAG-limited circuits (where the T₈₀ hits the upper limit) will result in the ball mill over-grinding unless (in the case of a variable speed mill) the ball mill speed is reduced to control the grind size. Ball-limited circuits (where the T₈₀ hits the lower limit) will result in the charge level in the SAG mill dropping until its power draw matches the throughput limit dictated by the ball mill. It is important to realize that once the SAG mill charge level drops below the ball charge, it can no longer empty and the mill power draw will be incalculable and an error message will appear.

Circuits that operate at or near the transfer size limits should be less efficient than the default formulas will estimate. If you have a design that is consistently operating around the limits, then consider adding a contingency to inflate the specific energy consumption estimates to account for this poor grinding efficiency. Alternatively, if you are designing a new circuit then choose a different combination of SAG and ball mills that operates in a more reasonable transfer size range.

The rod mill oversize feed factor (EF₄^RM) in the Barratt E_SAG equation is calculated using the greater of the sample's rod mill or crushing work index. The optimal feed size and EF₄ are both calculated using whichever is greater.

The ball mill oversize feed factor (EF₄^BM) is always calculated with the ball mill work index. The optimal feed size for the EF₄^BM is always calculated using the rod mill work index.

Recommended Usage

This model should be the upper end-member of the range of Bond/Barratt style models. It is useful when interpreting pilot plant results to determine where the pilot plant results fall relative to the spectrum of models. It can also be used as an extra-conservative model for design work.

Because this model does not include an internal phantom cyclone mechanism, it is customary to include an allowance for it in the CF_ball factor by using a value of 0.95 (some fines in SAG product) to 0.85 (many fines in SAG product). If a SAG product does not include extra fines versus a standard size distribution, then use a value of 1.00.

Default parameter values

• Maximum transfer size, µm = 6000
• Minimum transfer size, µm = 400 ^{[Starkey et al. 2008]}
• Hypothetical tertiary crusher product size, µm = 18850 ^{[Barratt 1979]}
• Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P₈₀ and typical ball mill work index test F₈₀).