Nordberg ball mill model

This ball mill power draw model is based on a torque model and empirical measurements made by the Nordberg Equipment Company for use by its sales representatives to size grinding mills. Slight differences in the equations used allow rod mills, dry ball mills and wet overflow and grate ball mills to be sized.

History

This model was published by the Nordberg equipment company with versions of it appearing in their "Red Book" equipment sizing manual in the 1970's. The latest version of this model published was by the Outokumpu company (now Outotec) publication "The Science of Comminution" (undated, but probably about 2002).

Inputs

The model requires three inputs in its original form, and a "density corrected" variation includes a fourth input.

• mill effective inside diameter (to calculate Factor A)
• mill fraction filling of the charge (to calculate Factor B)
• mill fraction of critical speed (to calculate Factor C).
• (for density correction) effective density of the mill charge

Output

The model output is the "US horsepower per foot of mill length" where the power is measured at the mill shell. Multiplying this output by the mill effective grinding length and converting the result to modern units of power results in the mill power draw at the shell in kilowatts.

Calculation description

Each of the three original inputs are fit to equations based on the Nordberg published tables that generate, respectively, values for Factor A, Factor B and Factor C which are multiplied together. There are slightly different versions of the Factor B for different styles of mills. The equation presented below is for wet overflow ball mills.

$Factor A = 10^{2.499 \times Log10(inside diam, mm) - 6.957}$

$Factor B = min(5.2 , 5.2-10^{1.951 \times Log10(50-MillLoad) - 2.66}$

$Factor C = 10^{0.009 \times speed - 1.412}$

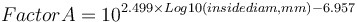
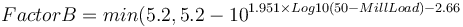
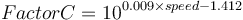
The Outokumpu reference gives the base mill charge density for these formulae as 310 lb/ft³. This translates to a charge density of 5050 kg/m³. Knowing the actual density of the charge allows the correction to be calculated as:

<math>\text{Density correction} = \frac{\text{actual density } kg/m^3}{5050 kg/m^3}