Ball mill work index adjustment

Ball mill work index adjustment

The Bond ball mill work index test requires the operator to select an appropriate screen size to "close" the test. The procedure states that the closing screen size should be such that the product size of the test is the same as the expected product size of the operating plant. If the tests were done at the wrong closing screen size, then a ball mill work index adjustment procedure can be conducted as follows:

1. In the laboratory, select a series of samples, each suitable for performing three or more work index tests (probably 30 kg of sample is the practical minimum).
2. Conduct a series of work index determinations on each sample, but vary the closing screen mesh. At minimum, test two different closing mesh sizes (the closing size you did the original tests at, and the closing size that matches your new desired P80). Three or four different mesh sizes are better.
3. Calculate the specific energy of each ball mill test, E_ball = 10 × Wi (P80^-0.5 - F80^-0.5)
4. Fit the specific energy results for all BM tests, E_ball = K × P₈₀^-a. Use the power regression model or use logarithms to rearrange and solve for a and K using linear regression of the logarithms.
5. If there is a clear discontinuity in the work index at a particular size, this probably indicates a hard grain size is being encountered in the test. If this grain size is between your original test P80 and the desired, P80, just continue with the procedure. If this grain size is above or below the size range of interest, then exclude those sizes and repeat the regression.

The precise method used to do the adjustment is based on Josephin & Doll (2018).

• Compute K values for each grindability result:

$K = \frac{10 \times Wi_{test} \times (P_{80|test}^{-0.5} - F_{80}^{-0.5})}{P_{80|test}^{-a}}$

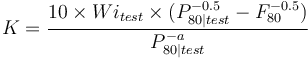
• Then compute the adjusted work index each grindability result using the K value:

$Wi_{adjusted} = \frac{K_{test} \times P_{80|adjusted}^{-a}}{10 \times (P_{80|adjusted}^{-0.5} - F_{80}^{-0.5})}$

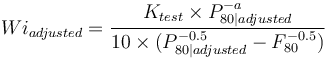
Morrell Mib adjustment

The Morrell Mi equations are generally of the form of Hukki's Conjecture, so the adjustment procedure is also valid for adjusting an Mib value to a different particle size if you have measured the ore's exponent a. It follow the similar process to the Wi correction where a Hukki exponent is determined in 3+ Bond ball mill work index determinations using Morrell's equation for the specific energy term, then Hukki's equation is solved for constant K at the tests' P₈₀ values $E = K \times P_{80|test}^{-a} = 4 \times Mib_{test} \times ( P_{80|test}^{-f(P_{80|test})} - F_{80}^{-f(F_{80})} )$

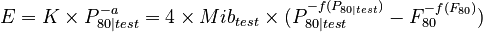
Comments

• When doing Bond/Barratt models, enter the exponent a into the Ball mill Wi adjust exponent (a) (drop the negative sign, a should always be positive when you enter it).
• This adjustment only applies to regular Bond ball mill work index tests. The model will ignore the adjustment for any sample identified as a "modified ball mill test" (where the ModBWI is set to a non-zero number).