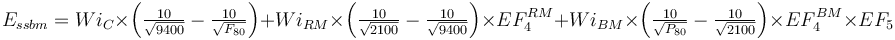Model:Bond-Rowland SSBM

Bond/Rowland Single Stage Ball Mill Model

This is a multi-stage crushing plant feeding a ball mill model that estimates the specific energy consumption (E_BM) using the Rowland interpretation of the classical Bond work index equation including Rowland efficiency factors.

$E_{ssbm} = Wi_{C} \times \left ( \tfrac {10}{\sqrt{ 9400 }} - \tfrac {10}{\sqrt{ F_{80} }} \right ) + Wi_{RM} \times \left ( \tfrac {10}{\sqrt{ 2100 }} - \tfrac {10}{\sqrt{ 9400 }} \right )\times EF_4^{RM} + Wi_{BM} \times \left ( \tfrac {10}{\sqrt{ P_{80} }} - \tfrac {10}{\sqrt{ 2100 }} \right ) \times EF_4^{BM} \times EF_5$ ^{Rowland, 2006}

$E_{total} = E_{crusher} + E_{ball}$

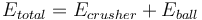
The rod mill oversize feed factor (EF₄^RM) is calculated using the greater of the sample's rod mill or crushing work index (which is usually the Wi_RM). The optimal feed size and EF₄ are both calculated using whichever is greater.

$EF_4^{RM} =\left [ 1 + \left( \frac{ (0.907 \times Wi_{RM} - 7) }{ \left (\frac{F_{80} }{ P_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 16 000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]$

where:

• F₈₀ = 9400 µm
• P₈₀ = 2100 µm

The ball mill oversize feed factor (EF₄^BM) is always calculated with the ball mill work index. The optimal feed size for the EF₄^BM is always calculated using the rod mill work index.

$EF_4^{BM} =\left [ 1 + \left( \frac{(0.907 \times Wi_{BM} - 7) }{ \left (\frac{F_{80} }{ P_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 4000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]$

where:

• F₈₀ = 2100 µm
• P₈₀ = the specified circuit product size, µm

Default parameter values

• Assumed crusher product P₈₀ size, µm = 9400
• Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P₈₀ and typical ball mill work index test F₈₀).