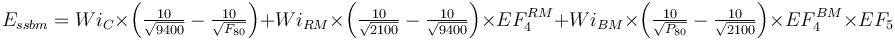Difference between revisions of "Model:Bond-Rowland SSBM"
(→Bond Single Stage Ball Mill Model) |
(→Default parameter values) |
||
| Line 31: | Line 31: | ||
* F<sub>80</sub> = 2100 µm |
* F<sub>80</sub> = 2100 µm |
||
* P<sub>80</sub> = the specified circuit product size, µm |
* P<sub>80</sub> = the specified circuit product size, µm |
||
| + | |||
| + | == Secondary and tertiary crushers == |
||
| + | |||
| + | The model '''does NOT validate''' the choice of crushers for the specified sizes; it simply calculates a specific energy based on the power drawn and the throughput dictated by the ball mill circuit. The throughput in the crushing circuit is NOT calculated and the motor sizes are NOT checked to see if they are suitable for the duty presented. |
||
| + | |||
| + | The choice of crushers and arrangement is normally based on volumetric flow and not on power draw. Use a crusher catalogue or another tool, like Metso's Bruno software, to determine the size and arrangement of the crushers ahead of the ball mill(s). |
||
== Default parameter values == |
== Default parameter values == |
||
| − | * Assumed crusher product |
+ | * Assumed crusher product (T<sub>80</sub>) size, µm = 9400 |
* Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P<sub>80</sub> and typical ball mill work index test F<sub>80</sub>). |
* Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P<sub>80</sub> and typical ball mill work index test F<sub>80</sub>). |
||
Revision as of 00:22, 8 May 2014
Bond/Rowland Single Stage Ball Mill Model
This is a multi-stage crushing plant feeding a ball mill model that estimates the specific energy consumption (EBM) using the Rowland interpretation of the classical Bond work index equation including Rowland efficiency factors.
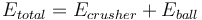
The rod mill oversize feed factor (EF4RM) is calculated using the greater of the sample's rod mill or crushing work index (which is usually the WiRM). The optimal feed size and EF4 are both calculated using whichever is greater.
![EF_4^{RM} =\left [ 1 + \left( \frac{ (0.907 \times Wi_{RM} - 7) }{ \left (\frac{F_{80} }{ P_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 16 000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]](/images/math/7/e/9/7e9b49234a38249bd7b36477cdc0e3ef.png)
where:
- F80 = 9400 µm
- P80 = 2100 µm
The ball mill oversize feed factor (EF4BM) is always calculated with the ball mill work index. The optimal feed size for the EF4BM is always calculated using the rod mill work index.
![EF_4^{BM} =\left [ 1 + \left( \frac{(0.907 \times Wi_{BM} - 7) }{ \left (\frac{F_{80} }{ P_{80}} \right )} \right) \left ( {\frac{F_{80} }{ { 4000 \left(\frac{14.33}{Wi_{RM} } \right )^{0.5}}} }-1 \right ) \right ]](/images/math/a/1/a/a1a63ddfd19337a26911b8e6354d94b3.png)
where:
- F80 = 2100 µm
- P80 = the specified circuit product size, µm
Secondary and tertiary crushers
The model does NOT validate the choice of crushers for the specified sizes; it simply calculates a specific energy based on the power drawn and the throughput dictated by the ball mill circuit. The throughput in the crushing circuit is NOT calculated and the motor sizes are NOT checked to see if they are suitable for the duty presented.
The choice of crushers and arrangement is normally based on volumetric flow and not on power draw. Use a crusher catalogue or another tool, like Metso's Bruno software, to determine the size and arrangement of the crushers ahead of the ball mill(s).
Default parameter values
- Assumed crusher product (T80) size, µm = 9400
- Hypothetical rod mill product size, µm = 2100 (mid-point of the range between typical rod mill work index test P80 and typical ball mill work index test F80).