Difference between revisions of "Phantom cyclone"
(→SAG mills and HPGRs) |
(→Other models) |
||
| Line 29: | Line 29: | ||
A plant survey will not return this 80% passing size; it contains the extra fines. One way to model this plant survey data is to mathematically pass the stream through a hydrocyclone and strip off the extra fines. The cyclone underflow stream should have a Bond-compatible size distribution which matches the Bond power-model transfer size. The ''phantom cyclone'' is named for this method of treating SAG product for modelling. |
A plant survey will not return this 80% passing size; it contains the extra fines. One way to model this plant survey data is to mathematically pass the stream through a hydrocyclone and strip off the extra fines. The cyclone underflow stream should have a Bond-compatible size distribution which matches the Bond power-model transfer size. The ''phantom cyclone'' is named for this method of treating SAG product for modelling. |
||
| − | == |
+ | ==Amelunxen SGI model== |
The [[Model:Amelunxen SGI|Amelunxen SG]]I model is calibrated for actual transfer size measurements from operating plants and do include the extra fines. The CFball calibration factor is used to "soak up" the extra fines when using an SGI model. |
The [[Model:Amelunxen SGI|Amelunxen SG]]I model is calibrated for actual transfer size measurements from operating plants and do include the extra fines. The CFball calibration factor is used to "soak up" the extra fines when using an SGI model. |
||
Latest revision as of 19:07, 29 August 2023
Phantom cyclone effect
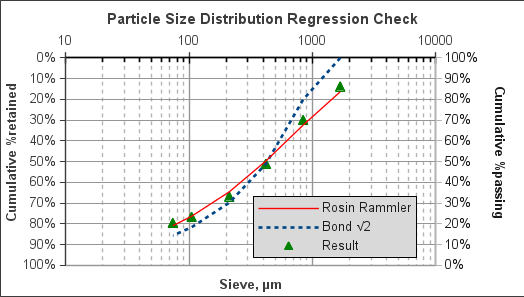
SAG and AG mills produce more fines, as a proportion of the whole particle size distribution, than more classical comminution machines such as rod mills. This causes a problem for power-based models because only a single point (the 80% passing point) is used as a proxy to represent the whole particle size distribution, and the whole distribution is assumed to be "normal".
Bond models
Fred Bond spends a lot of effort describing the shapes of particle size distribution curves in his Third Theory (Bond, 1952) and several earlier works. He sums up the intended shape of a size distribution for which is model is calibrated as:
Experience has shown that the average slope [...] of the size distribution percent passing [...] on a log-log plot of the percent passing against the sieve opening, is very close to 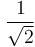 Bond, 1952
Bond, 1952
Bond also proposed this model of a particle size distribution:
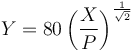
where: Y is the percent passing a size X and P is the 80% passing size (all sizes in µm).
Bond claims this model to be suitable for most of the crushing, rod milling and ball milling machines and applications that were surveyed by Bond and his colleagues in the 1940's and 1950's.
SAG mills and HPGRs
Autogenous and semi-autogenous grinding mills were not unknown during Bond's day, but they were relatively minor equipment that was used in a few boutique applications. The widespread adoption of SAG milling happened in the 1970's and 1980's, well after Bond's Third Theory was already established. High pressure grinding rolls (HPGR's) did not exist in a modern sense during Bond's day, and they were only adopted into the minerals industry from the very early part of the 21st century (although they existed earlier in the cement industry).
The problem with SAG mills and HPGRs, from a modelling sense, is that their particle size distributions do not follow Bond's specification; both have more fines in their product stream than Bond's specification of an "average" size distribution. There are a variety of ways to describe this phenomenon; arguably the most common terms are the phantom cyclone effect in SAG milling and microcracking in HPGRs (which are treated as the same effect for power-modelling purposes).
The Bond/Barratt models assume that the SAG mill product stream is a Bond-compatible size distribution, an the T80 predictions are presented on this basis and the extra fines are ignored (however, the Optimized Bond/Barratt models ball mills do reflect the reduction in operating work index).
A plant survey will not return this 80% passing size; it contains the extra fines. One way to model this plant survey data is to mathematically pass the stream through a hydrocyclone and strip off the extra fines. The cyclone underflow stream should have a Bond-compatible size distribution which matches the Bond power-model transfer size. The phantom cyclone is named for this method of treating SAG product for modelling.
Amelunxen SGI model
The Amelunxen SGI model is calibrated for actual transfer size measurements from operating plants and do include the extra fines. The CFball calibration factor is used to "soak up" the extra fines when using an SGI model.