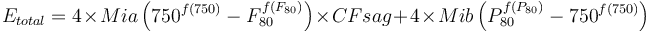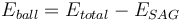Model:Morrell Mi SMC SAG

Morrell SMC SAG & ball mill Model

This is a SAG or AG mill plus ball mill model that estimates the specific energy consumption (E_SAG) using the equations of Morrell (2004).

Testwork Required

• The SMC™ test, stored in the "DWT" testwork table (SMC is a Drop Weight Test).
• Bond ball mill work index. The method requires all the elements of the ball mill work index test to be filled in:
  • Ball mill Wi test closing screen size, umclosing, µm
  • Ball mill Wi test product size, P₈₀, µm
  • Ball mill Wi test feed size, F₈₀, µm
  • Ball mill Wi grams per revolution at test conclusion, gpr

Required parameters

• F₈₀, µm is the 80% passing size of the fresh feed to the circuit (expected to be a Bond-compatible size distribution).
• P₈₀, µm is the 80% passing size of the circuit product (expected to be a Bond-compatible size distribution).
• Availability, expressed as a decimal (0.90 = 90% availability) is used to convert t/h to t/d.
• Ball mill Operating strategy when circuit is SAG-limited (note, fixed speed ball mills can only be vary P₈₀)

Optional parameters

• Description and Comment are optional text fields
• Maximum t/h limit is a t/h throughput above which a warning message is displayed (but does not actually limit the throughput).
• T₈₀ min and T₈₀ min override the transfer size restrictions built into the model
• Ball mill work index adjustment used to adjust Wi_BM for different P₈₀ sizes.
  • coefficient (a), the fitted coefficient to the adjustment equation
  • exponent (b), the fitted exponent to the adjustment equation
• CFsag calibration factor, model tuning factor for E_ASAG

Formulae

The method is superficially similar to Bond (among other models), but with a variable exponent on size defined by:

$f(x) = - 0.295 - \frac{x}{10^6}$

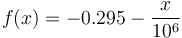
Where x is the particle 80% passing size in µm.

$E_{total} = 4 \times Mia \left( 750^{f(750)} - F_{80}^{f(F_{80})} \right) \times CFsag + 4 \times Mib \left( P_{80}^{f(P_{80})} - 750^{f(750)} \right)$^{Morrell, 2004}

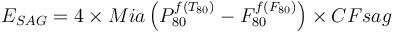$E_{SAG} = 4 \times Mia \left( P_{80}^{f(T_{80})} - F_{80}^{f(F_{80})} \right) \times CFsag$^{based on Doll 2013, but note Morrell, 2011}

$E_{ball} = E_{total} - E_{SAG}$^{Morrell, 2004}

CF_sag calibration factor

The CF_sag factor is used to reflect the effect of pebble crushing on the overall circuit performance. This value is automatically selected if you leave this field blank in the model configuration settings.

• Base value, SAB circuit (no pebble crushing, ~6 inch SAG feed), CF_sag = 1.00
• Pebble crushing, SABC circuit, CF_sag = 0.95

Transfer size

Morrell specifically discourages use of transfer size in calculations such as those in SAGMILLING.COM for a variety of reasons (see discussion in Morrell, SAG 2011). Unfortunately, the alternative method proposed by Morrell is an equation that requires pre-selected mill sizes and a series of unpublished calibration factors. This alternative method is not practical for the calculations in SAGMILLING.COM, so a transfer size approach is used instead.

The modelled transfer sizes are "Bond-compatible" and not similar to what would be measured directly in a plant survey. Plant survey results would need to be subjected to a phantom cyclone calculation before they are comparable to the model predictions.