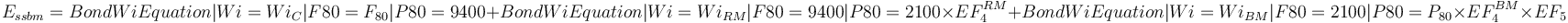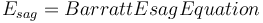Difference between revisions of "Model:Bond/Barratt SABC Models"
(Created page with "== Bond/Barratt Specific Energy Consumption Model == blah, blah, blah The model assumes that the calculated value of E<sub>ssbm</sub> + the specified contingency is greater ...") |
(→Bond/Barratt Specific Energy Consumption Model) |
||
| Line 1: | Line 1: | ||
== Bond/Barratt Specific Energy Consumption Model == |
== Bond/Barratt Specific Energy Consumption Model == |
||
| + | This is a SAG or AG mill plus ball mill model that estimates the overall circuit specific energy consumption using the classical Bond work index equation for multi-stage crushing and single-stage ball milling (E<sub>ssbm</sub>) including Rowland efficiency factors. The circuit E<sub>total</sub> is equal to the E<sub>ssbm</sub> plus an inefficiency factor (CF) related to the difference in grinding efficiency of the two types of circuits. The SAG mill specific energy consumption (E<sub>SAG</sub>) is calculated using the 1979 Barratt equation and the ball mill specific energy consumption (E<sub>bm</sub>) |
||
| − | blah, blah, blah |
||
| + | |||
| + | This model includes a [[phantom cyclone]] effect in the equations due to the ball mill being calculated by difference and not being calculated by the normal Bond equation. The resultant operating work index of the ball mill will vary according to the ratio of the ball mill, rod mill and crushing work index values and is in the range of 80% of the measured ball mill work index value. |
||
| + | |||
| + | <math> E_{ssbm} = {{BondWiEquation|Wi=Wi_{C}|F80=F_{80}|P80=9400 }} + {{BondWiEquation|Wi=Wi_{RM}|F80=9400|P80=2100 }}\times EF_4^{RM} + {{BondWiEquation|Wi=Wi_{BM}|F80=2100|P80=P_{80} }} \times EF_4^{BM} \times EF_5</math> <sup>[[Bibliography:_Specific_energy_consumption_models|Rowland, 2006]]</sup> |
||
| + | |||
| + | <math> E_{total} = E_{ssbm} \times (1+CF) </math> |
||
| + | |||
| + | <math> E_{sag} = {{BarrattEsagEquation}} </math> |
||
| + | <sup>[[Bibliography:_Specific_energy_consumption_models|Barratt, 1989]]</sup> |
||
| + | |||
| + | <math> E_{bm}= E_{total} - E_{sag}</math> |
||
| + | |||
| + | As with most models, the power split between the SAG and ball mills is evaluated and the transfer size (T<sub>80</sub>) necessary to balance the power draw between the two stages is estimated. If that transfer size is within the specified limits, then the calculation proceeds to calculate the E<sub>SAG</sub> and E<sub>bm</sub> using that transfer size. If the transfer size to balance the power is outside the specified limits, then the transfer size size is forced to the limit and the E<sub>SAG</sub> and E<sub>bm</sub> values are then calculated. SAG-limited circuits (where the T<sub>80</sub> hits the upper limit) will result in the ball mill over-grinding unless the ball mill speed is reduced to control the grind size (in the case of a variable speed mill). Ball-limited circuits (where the T<sub>80</sub> hits the lower limit) will result in the charge level in the SAG mill dropping until its power draw matches the throughput limit dictated by the ball mill. It is important to realize that once the SAG mill charge level drops to be equal to the ball charge, the model will be operating "out of range" and the predictions will not be valid. |
||
| + | |||
| + | Circuits that operate at or near the transfer size limits should be less efficient than the default formulas will estimate. If you have a design that is consistently operating around the limits, then consider adding a contingency to inflate the specific energy consumption estimates to account for this poor grinding efficiency. Alternatively, if you are designing a new circuit then choose a different combination of SAG and ball mills that operates in a more reasonable transfer size range. |
||
| + | |||
| + | The rod mill oversize feed factor (EF<sub>4</sub><sup>RM</sup>) in the Barratt E<sub>SAG</sub> equation is calculated using the greater of the sample's rod mill or crushing work index. The optimal feed size and EF<sub>4</sub> are both calculated using whichever is greater. The ball mill oversize feed factor (EF<sub>4</sub><sup>BM</sup>) is always calculated with the ball mill work index. |
||
The model assumes that the calculated value of E<sub>ssbm</sub> + the specified contingency is greater than the sum of E<sub>sag</sub> + E<sub>peb</sub>; otherwise E<sub>bm</sub> will be negative. The model does a check to see if E<sub>bm</sub> calculated is negative and, if so, will substitute the [[Raw Bond Model]] equation estimate for E<sub>bm</sub>. |
The model assumes that the calculated value of E<sub>ssbm</sub> + the specified contingency is greater than the sum of E<sub>sag</sub> + E<sub>peb</sub>; otherwise E<sub>bm</sub> will be negative. The model does a check to see if E<sub>bm</sub> calculated is negative and, if so, will substitute the [[Raw Bond Model]] equation estimate for E<sub>bm</sub>. |
||
| + | |||
| + | === Discussion, pebble crushing === |
||
| + | The pebble crusher is assumed to be part of the SAG mill for the purposes of this calculation. E<sub>peb</sub> is calculated as the power drawn by the pebble crusher divided by the circuit throughput. This E<sub>peb</sub> is then deducted from E<sub>sag</sub>. |
||
| + | |||
| + | The total circuit specific energy consumption is generally higher when no pebble crusher is present in a circuit. The rule of thumb is apply the CF value of 0.15 for SAB circuits (5% higher overall specific energy consumption). |
||
| + | |||
| + | === Discussion, Rowland EF factors === |
||
| + | The model is only interested in the EF factors that are properties of the rock, namely the coarse feed EF4 factor and the fine product EF5 factor. The EF factors that correspond to machine characteristics are not included (EF<sub>1</sub>, EF<sub>2</sub>, EF<sub>3</sub>, EF<sub>6</sub>, EF<sub>7</sub> and EF<sub>8</sub>) as they are intended to capture the inefficiency of certain types of milling circuits. The assumption in this model is that the E<sub>ssbm</sub> is the "maximum efficiency" possible for a grinding circuit, and therefore one can neglect the machine characteristics. |
||
=== Model defaults === |
=== Model defaults === |
||
* Maximum T<sub>80</sub>, µm = 6000 |
* Maximum T<sub>80</sub>, µm = 6000 |
||
* Minimum T<sub>80</sub>, µm = 400 |
* Minimum T<sub>80</sub>, µm = 400 |
||
| + | * CF factor on E<sub>ssbm</sub> = 0.10 |
||
Revision as of 21:39, 14 November 2012
Contents
Bond/Barratt Specific Energy Consumption Model
This is a SAG or AG mill plus ball mill model that estimates the overall circuit specific energy consumption using the classical Bond work index equation for multi-stage crushing and single-stage ball milling (Essbm) including Rowland efficiency factors. The circuit Etotal is equal to the Essbm plus an inefficiency factor (CF) related to the difference in grinding efficiency of the two types of circuits. The SAG mill specific energy consumption (ESAG) is calculated using the 1979 Barratt equation and the ball mill specific energy consumption (Ebm)
This model includes a phantom cyclone effect in the equations due to the ball mill being calculated by difference and not being calculated by the normal Bond equation. The resultant operating work index of the ball mill will vary according to the ratio of the ball mill, rod mill and crushing work index values and is in the range of 80% of the measured ball mill work index value.
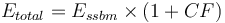
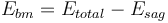
As with most models, the power split between the SAG and ball mills is evaluated and the transfer size (T80) necessary to balance the power draw between the two stages is estimated. If that transfer size is within the specified limits, then the calculation proceeds to calculate the ESAG and Ebm using that transfer size. If the transfer size to balance the power is outside the specified limits, then the transfer size size is forced to the limit and the ESAG and Ebm values are then calculated. SAG-limited circuits (where the T80 hits the upper limit) will result in the ball mill over-grinding unless the ball mill speed is reduced to control the grind size (in the case of a variable speed mill). Ball-limited circuits (where the T80 hits the lower limit) will result in the charge level in the SAG mill dropping until its power draw matches the throughput limit dictated by the ball mill. It is important to realize that once the SAG mill charge level drops to be equal to the ball charge, the model will be operating "out of range" and the predictions will not be valid.
Circuits that operate at or near the transfer size limits should be less efficient than the default formulas will estimate. If you have a design that is consistently operating around the limits, then consider adding a contingency to inflate the specific energy consumption estimates to account for this poor grinding efficiency. Alternatively, if you are designing a new circuit then choose a different combination of SAG and ball mills that operates in a more reasonable transfer size range.
The rod mill oversize feed factor (EF4RM) in the Barratt ESAG equation is calculated using the greater of the sample's rod mill or crushing work index. The optimal feed size and EF4 are both calculated using whichever is greater. The ball mill oversize feed factor (EF4BM) is always calculated with the ball mill work index.
The model assumes that the calculated value of Essbm + the specified contingency is greater than the sum of Esag + Epeb; otherwise Ebm will be negative. The model does a check to see if Ebm calculated is negative and, if so, will substitute the Raw Bond Model equation estimate for Ebm.
Discussion, pebble crushing
The pebble crusher is assumed to be part of the SAG mill for the purposes of this calculation. Epeb is calculated as the power drawn by the pebble crusher divided by the circuit throughput. This Epeb is then deducted from Esag.
The total circuit specific energy consumption is generally higher when no pebble crusher is present in a circuit. The rule of thumb is apply the CF value of 0.15 for SAB circuits (5% higher overall specific energy consumption).
Discussion, Rowland EF factors
The model is only interested in the EF factors that are properties of the rock, namely the coarse feed EF4 factor and the fine product EF5 factor. The EF factors that correspond to machine characteristics are not included (EF1, EF2, EF3, EF6, EF7 and EF8) as they are intended to capture the inefficiency of certain types of milling circuits. The assumption in this model is that the Essbm is the "maximum efficiency" possible for a grinding circuit, and therefore one can neglect the machine characteristics.
Model defaults
- Maximum T80, µm = 6000
- Minimum T80, µm = 400
- CF factor on Essbm = 0.10