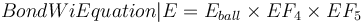Model:Raw Bond/Barratt SAB & SABC Model

Raw Bond Model

This is a SAG or AG mill plus ball mill model that estimates the specific energy consumption (E_SAG) using the 1979 Barratt equation and the classical Bond work index equation including Rowland efficiency factors. The model allows a manual calibration factor on both equations (CF_SAG and CF_ball, respectively).

This formula usually gives higher total circuit specific energy consumption estimates than the other Bond/Barratt models. This is largely due to the absence of a phantom cyclone effect in the equations.

E_{SAG} = \left [ \left (

Wi_{C}   \times \left ( \frac {10}{\sqrt{ P_{C}  }} - \frac {10}{\sqrt{ F_{80}  }} \right ) + 
Wi_{RM} \times \left ( \frac {10}{\sqrt{ P_{R}  }} - \frac {10}{\sqrt{ P_{C}  }} \right ) \times EF_4^{RM} + 
Wi_{BM} \times \left ( \frac {10}{\sqrt{110} } - \frac {10}{\sqrt{ P_{R}  }} \right ) \times EF_4^{BM}

\right )\times 1.25 - Wi_{BM} \times \left ( \frac {10}{\sqrt{ {110} }} - \frac {10}{\sqrt{ T_{80} }} \right ) \right ]

${{BondWiEquation|E=E_{ball} }} \times EF_4 \times EF_5$^{Rowland, 2006}

$E_{total} = CF_{SAG} \times E_{SAG} + CF_{ball} \times E_{ball}$

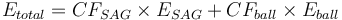
Recommended Usage

This model should be the upper end-member of the range of Bond/Barratt style models. It is useful when interpreting pilot plant results to determine where the pilot plant results fall relative to the spectrum of models. It can also be used as an extra-conservative model for design work.

Because this model does not include an internal phantom cyclone mechanism, it is customary to include an allowance for it in the CF_ball factor by using a value of 0.95 (some fines in SAG product) to 0.85 (many fines in SAG product). If a SAG product does not include extra fines versus a standard size distribution, then use a value of 1.00.

Default parameter values

• Maximum transfer size, µm = 6000
• Minimum transfer size, µm = 400 ^{[Starkey et al.]}