Work Index

Bond Work Index

The Bond Work Index is an empirical calibration of comminution equipment specific energy consumption at different size classes. Three types of work index are ore hardness laboratory tests that can be used to design industrial grinding equipment.

There are five types of Work Index:

Ball mill work index

This is a laboratory measurement used to determine the ore grindability in the particle size range typically encountered by ball mills. Testwork:_Bond_ball_mill_work_index

Rod mill work index

This is a laboratory measurement used to determine the ore grindability in the particle size range typically encountered by rod mills, which were common grinding equipment in the mid twentieth century. Testwork:_Bond_rod_mill_work_index

Crushing work index

Also called the Low Energy Impact Test (LEIT), this is a laboratory measurement used to determine the ore crusability in the particle size range typically encountered by cone crushers. Testwork:_Bond_crushing_work_index

Operating work index

This is a generic work index measured on an arbitrary piece of comminution equipment. Computing the operating work index requires the following measurements for the equipment:

• the fresh feed rate in dry tonnes per hour (excluding any circulating load), t/h
• the mechanical power consumed by the equipment at the equipment input (kW at the mill shell or pinion), kW
• the fresh feed 80% passing size in µm, F₈₀
• the classified product 80% passing size in µm, P₈₀

The Operating Work Index (Wi_O) is calculated as follows:

$Wi_{O} = \frac{kW / (t/h)}{10 \times \left(P_{80}^{-0.5} - F_{80}^{-0.5} \right)}$

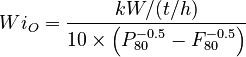
Work Index (generic)

The most generic definition of Work Index is that it is one-tenth of the coefficient of the special case of the Hukki Conjecture where the exponent is fixed at –½. The Hukki Conjecture is a continuum of grindability models that link the Work Index to other models like the SGI model, Rittinger, Kick, and Signature Plots.

The Units of Work Index

The modern units of work index are kW·h·µm^½·tonne^-1 and are distinct from Specific Energy Consumption (kWh/t).

The unfortunate common practice in the industry is to give Work Index the same units as specific energy consumption, specifically kWh/t. This is due to how the Third Theory equation was empirically calibrated and does not reflect the underlying physics.

The Third Theory equation is: $E = \frac{kW}{(t/h)} =10 \times Wi \times \left(P_{80}^{-0.5} - F_{80}^{-0.5} \right)$

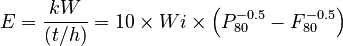
• If the 10 in the Third Theory is interpreted as the square-root of 100, a "typical product size" of ball milling operations,
• then the units of the size term (P₈₀^-½-F₈₀^-½) cancel the units of the coefficient (10).

This has the unwanted suggestion that Work Index is additive with Specific Energy Consumption, which it is not. Errors in technical documents have been caused by inexperienced engineers making this mistake. To prevent this error in the future, it is suggested that the interpretation of work index change so that the units are distinct from Specific Energy Consumption, as follows:

• the 10 is a unitless scaling factor
• the Work Index be treated as a coefficient related to the derivative of Specific Energy Consumption with particle size.

In this interpretation, the units of work index become kW·h·µm^½·t^-1. The values obtained will be relative to the type of ton/tonne measured; the original work by Bond was performed in US short tons (907 kg) or US long tons (1016 kg), but all modern work uses the basis of metric tonnes (1000 kg).